Обработка результатов косвенных измерений
Пусть искомая физическая величина y связана с другими величинами x 1, x 2,..., xn некоторой функциональной зависимостью
y = f (x 1, x 2,..., xn). (5)
Среди величин x 1, x 2,..., xn имеются величины, полученные при прямых измерениях, и табличные данные. Требуется определить абсолютную ∆ y и относительную e погрешности величины y. В большинстве случаев проще сначала вычислить относительную погрешность, а затем - абсолютную. Из теории вероятностей относительная погрешность косвенного измерения
Здесь Если какие-либо из слагаемых в выражении (6) меньше на порядок (в 10 раз) других слагаемых, то ими можно пренебречь. Это нужно учитывать при выборе табличных величин (p, g и др.), входящих в формулу относительной погрешности. Конечный результат записывается в виде:
y = < y > ± D y.
Здесь < y > - среднее значение косвенного измерения, полученное по формуле (5) при подстановке в нее средних величин xi, а ∆ y -абсолютная погрешность косвенного измерения, найденная из определения относительной погрешности
|

 . (6)
. (6)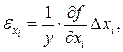 где
где  - частная производная функции по переменной xi, при вычислении которой все величины, кроме xi, считаются постоянными; ∆ xi - абсолютная погрешность величины xi. Если xi получена в результате прямых измерений, то ее среднее значение < x > и абсолютную погрешность ∆ x вычисляют по формулам (1) и (3). (Эти величины можно найти при помощи многофункционального калькулятора. Как это сделать смотрите в приложении.) Для всех измеренных величин xi задается одинаковая доверительная вероятность a.
- частная производная функции по переменной xi, при вычислении которой все величины, кроме xi, считаются постоянными; ∆ xi - абсолютная погрешность величины xi. Если xi получена в результате прямых измерений, то ее среднее значение < x > и абсолютную погрешность ∆ x вычисляют по формулам (1) и (3). (Эти величины можно найти при помощи многофункционального калькулятора. Как это сделать смотрите в приложении.) Для всех измеренных величин xi задается одинаковая доверительная вероятность a.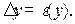 Обычно в абсолютной погрешности оставляют одну значащую цифру, а измеренную величину округляют до того разряда, в котором находится значащая цифра абсолютной погрешности.
Обычно в абсолютной погрешности оставляют одну значащую цифру, а измеренную величину округляют до того разряда, в котором находится значащая цифра абсолютной погрешности.


