Измерения и обработка результатов. В данной работе моделирование случайной величины осуществляется следующим образом
В данной работе моделирование случайной величины осуществляется следующим образом. При помощи обычных часов с секундной стрелкой задают некоторый промежуток времени t и измеряют его высокочувствительным цифровым частотомером или электрическим секундомером, вручную нажимая кнопки "старт" и "стоп". Выполнять работу рекомендуется двум студентам. Первый многократно задает определенные промежутки времени по часам, подавая команду "старт" и "стоп". Второй нажимает кнопки и записывает отсчеты по прибору. В этом случае результаты измерений будут независимыми, что должно привести к нормальному (Гауссовому) распределению случайной величины. 1. Проведите 30-50 раз измерение выбранного промежутка времени. Можно задать промежуток времени от 5 до 10 секунд. Показания цифрового частотомера занесите во второй столбец табл. 1. 2. Найдите в табл. 1 наименьший t min и наибольший t max из результатов наблюдений. Промежуток (t min - t max) разбейте на 6 - 10 равных интервалов Δ t. Границы интервалов занесите в табл. 2. 3. Подсчитайте число результатов наблюдений в табл. 2, попавших в каждый интервал Δ ti, и заполните второй столбец табл. 2. 4. Вычислите опытные значения плотности вероятности попадания случайной величины в каждый из интервалов Δ ti . Заполните третий столбец табл. 2. Таблица 1
5. Постройте гистограмму (рис. 1), для чего по оси абсцисс откладывайте интервалы Δ ti, являющиеся основаниями прямоугольников, высота которых равна плотности вероятности ρ i.
Таблица 2
6. Вычислите <t>; по (3) и s по (4). Можно воспользоваться результатами двадцати наблюдений. Полученные значения занесите в табл. 1. 7. По формуле (5) найдите максимальное значение плотности вероятности rmax при t = <t>;. Результаты занести в табл. 1. Сравнить полученные значения rmax с наибольшей высотой гистограммы. 8. Для значений t, соответствующих границам выбранных интервалов, вычислите по функции Гаусса (1) значения плотности вероятности r(t) и занесите их в четвертый столбец табл. 2. 9. Нанесите все расчетные точки на график, на котором изображена гистограмма, и проведите через них плавную кривую. Сравните их. В чем причина неполного соответствия кривой Гаусса и гистограммы? 10. Проверьте, насколько точно выполняется в опытах соотношение (1). Вычислите границы интервалов, указанных в первом столбце табл. 3. По данным табл. 1 подсчитайте число наблюдений N 12, попадающих в каждый из трех интервалов, а также отношение N 12/ N (6). Сравните их с известными значениями Р 12, соответствующими нормальному распределению случайных величин (1). В чем причина небольшого расхождения?
Таблица 3
|

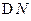
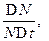 с-1
с-1



