Действия с приближенными числами
Многие считают, чем больше цифр содержит вычисленная или измеренная величина, тем она точнее. Вопрос о различной точности вычисления очень важен, так как завышение точности вычисления приводит к большому объему ненужной работы. Студенты часто вычисляют искомую величину с точностью до пяти и более значащих цифр. Следует понимать, что эта точность излишняя. Нет никакого смысла вести вычисления дальше того предела точности, который обеспечивается точностью определения непосредственно измерявшихся величин. Проведя обработку измерений, часто не подсчитывают ошибки отдельных результатов и судят об ошибке приближенного значения величины, указывая количество верных значащих цифр в этом числе. Значащими цифрами приближенного числа называются все цифры, кроме нуля, а также нуль в двух случаях: 1. когда он стоит между значащими цифрами (например, в числе 1071 - четыре значащих цифры); 2. когда он стоит в конце числа и когда известно, что единица соответствующего разряда в данном числе не имеется. Пример. В числе 5,20 три значащих цифры, и это означает, что при измерении мы учитывали не только единицы, но и десятые, и сотые, а в числе 5,2 - только две значащих цифры, и это значит, что мы учитывали только целые и десятые. При вычислении промежуточных результатов сохраняют на одну цифру больше, чем рекомендуют правила (так называемая запасная цифра). Её обычно пишут меньшим размером. В окончательном результате запасная цифра отбрасывается. Если она окажется меньше пяти, ее следует просто отбросить, а если пять или больше пяти, то, отбросив ее, следует предыдущую цифру увеличить на единицу. Обычно в абсолютной ошибке оставляют одну значащую цифру, а измеренную величину округляют до того разряда, в котором находится значащая цифра абсолютной ошибки. Приближенные вычисления следует производить с соблюдением следующих правил: 1. При сложении и вычитании в результате сохраняют столько десятичных знаков, сколько их содержится в числе с наименьшим количеством десятичных знаков. Например: 0,8934 + 3,24 + 1,188 = 0,893 + 3,24 + 1,188 = 5,321 ≈ 5,32. Сумму следует округлить до сотых долей, т.е. принять равной 5,32. 2. При умножении и делении в результате сохраняют столько значащих цифр, сколько их имеет приближенное число с наименьшим количеством значащих цифр. Например, необходимо перемножить 8,632´2,8´3,53. Вместо этого выражения следует вычислять 8,63´2,8´3,53 = 85,3 ≈ 85. 3. Результат расчета значений функций xn,
Рассмотрим пример. Пусть необходимо вычислить плотность вещества ρ, из которого изготовлен цилиндр. По определению
где m – масса тела, а V - его объём. Объём цилиндра определяется формулой
Здесь D - диаметр цилиндра, H - его высота. Следовательно, расчётная формула для плотности вещества будет иметь вид
Пусть D и H измерены штангенциркулем с ценой деления 0,1 мм, а масса определена на физических весах. В результате многократных измерений найдем средние значения < H > = 10,34 мм и < D > = 40,27 мм, а m = 35,9 г. При подстановке этих данных в формулу (7) получим
где D D и D H - абсолютные погрешности прямых измерений диаметра и высоты, а затем определить абсолютную погрешность плотности вещества из выражения ∆ρ = eρ. Пусть случайные абсолютные погрешности оказались равными: D D сл.= 0,01 мм; D H сл.= 0,23 мм, а ∆ m = 0,05 г. Сравним вычисленные случайные погрешности с аппаратурной, равной цене деления штангенциркуля. D D сл.<0,1, поэтому в формулу (8) подставим D D = 0,1 мм. А так как (D H сл./D H ап.)<3, то D H вычисляем по формуле (3) и получаем 0,25 мм. Значение p нужно выбрать таким, чтобы относительной погрешностью Δπ/π в формуле (8) можно было пренебречь. Из анализа измеренных величин и вычисленных абсолютных погрешностей D D и D H видно, что наибольший вклад в относительную погрешность измерения объема вносит ошибка измерения высоты. Вычисление относительной ошибки высоты дает eH = 0,0057. Если взять p = 3,1, то ep = 0,013, что превышает eH. Следовательно, значение p нужно взять 3,14. В этом случае Δπ/π» 0,00064 (Dp = 3,142-3,14 = 0,002),что значительно меньше eH и относительную погрешность p можно не учитывать. Вычисления относительной погрешности плотности по формуле (8) даёт значение e = 0,00769, а ∆ρ = 0,0077·2,72· 103 = 20,9 кг/м3. Так как в абсолютной погрешности принято оставлять одну значащую цифру, то конечный результат следует записать в виде:
ρ = (2,72 ± 0,02)103 кг/м3.
Необходимо сделать вывод по ответу. Полученное экспериментально значение величины плотности вещества равное 2,72·103 кг/м3 с точностью до ошибки измерений составляющей ± 0,02·103 кг/м3 совпадает с табличным (теоретическим) значением плотности алюминия равное 2,71·103 кг/м3. Текст, выделенный курсивом, является шаблоном вывода по ответу в любой лабораторной работе. Примечания:
1. Если измерения производят один раз или результаты многократных измерений одинаковы, то за абсолютную погрешность измерений нужно взять аппаратурную погрешность, которая для большинства используемых приборов равна цене деления прибора (более подробно об аппаратурной погрешности см. в разделе “Измерительные приборы”). 2. Если табличные или экспериментальные данные приводятся без указания погрешности, то абсолютную погрешность таких чисел принимают равной половине порядка (разряда) последней значащей цифры. Например, если m = 2,47 г, тогда Δ m = 0,5·0,01 = 0,005 г.
|

 , lg (x) некоторого приближенного числа x должен содержать столько значащих цифр, сколько их имеется в числе x. Например:
, lg (x) некоторого приближенного числа x должен содержать столько значащих цифр, сколько их имеется в числе x. Например: .
.
 .
. (7)
(7)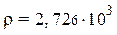 кг/ м3. Если эту величину считать окончательным результатом, то запасная цифра 6 отбрасывается. Абсолютная погрешность измерения плотности в этом случае будет равна половине единицы последнего разряда, т.е. 5 кг/м3. Так обычно поступают при однократном измерении. В данном примере Н и D измерялись несколько раз, поэтому сначала надо вычислить относительную погрешность косвенного измерения плотности вещества по формуле
кг/ м3. Если эту величину считать окончательным результатом, то запасная цифра 6 отбрасывается. Абсолютная погрешность измерения плотности в этом случае будет равна половине единицы последнего разряда, т.е. 5 кг/м3. Так обычно поступают при однократном измерении. В данном примере Н и D измерялись несколько раз, поэтому сначала надо вычислить относительную погрешность косвенного измерения плотности вещества по формуле (8)
(8)


