Описание установки и метода измерений. Металлический шар 1 подвешен на тонкой проволоке (рис
По второму закону Ньютона средняя сила взаимодействия, возникающая в момент удара шара о стенку,
где m - масса шара;
Исключим из формулы (1) скорости u и u. Скорость шара u перед ударом можно вычислить, если знать угол a, определяемый по шкале 4, который образует нить подвеса шара с ее вертикальным положением до удара (рис 1). По закону сохранения энергии
здесь h - высота, на которую поднят шар; u - скорость шара перед ударом. Тогда
Из рис. 1 следует, что
откуда
где l - расстояние от точки подвеса шара до его центра. Следовательно,
После удара шар отскочит от плиты и поднимется на высоту h', нить подвеса отклонится от вертикального положения на некоторый угол g. По закону сохранения энергии
Аналогично (2) определим скорость шара после удара:
Подставив (2) и (3) в (1),получим
Формула (4) является расчетной. Уменьшение угла отклонения нити подвеса шарика после удара его о плиту происходит потому, что удар не является абсолютно упругим, и часть механической энергии превращается во внутреннюю энергию соударяющихся тел. Потери механической энергии при ударе характеризуются коэффициентом восстановления скорости K c. Коэффициент восстановления скорости K c в случае удара шара о массивную стенку определяется по формуле
Подставим (2) и (3) в (5), получим расчетную формулу для определения коэффициента восстановления
В условиях опыта коэффициент восстановления скорости можно считать величиной, зависящей только от материала соударяющихся тел. Посредством K c можно характеризовать упругие свойства того или иного материала. Очевидно, для реальных тел всегда K c<1.
|

 Металлический шар 1 подвешен на тонкой проволоке (рис. 1). При вертикальном положении нити шар 1 почти касается одной из двух противоположных сторон массивной металлическойплиты 2 (стороны плиты изготовлены из разных материалов). В момент удара шара о плиту замыкается электрическая цепь. Продолжительность удара шара о плиту определяют электроннымсекундомером 3 по времени замыкания шаром электрической цепи.
Металлический шар 1 подвешен на тонкой проволоке (рис. 1). При вертикальном положении нити шар 1 почти касается одной из двух противоположных сторон массивной металлическойплиты 2 (стороны плиты изготовлены из разных материалов). В момент удара шара о плиту замыкается электрическая цепь. Продолжительность удара шара о плиту определяют электроннымсекундомером 3 по времени замыкания шаром электрической цепи.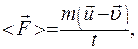
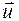 - скорость шара после удара;
- скорость шара после удара; 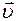 - скорость шара перед ударом; t - время соударения. Скорость шара
- скорость шара перед ударом; t - время соударения. Скорость шара 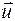 после удара о плиту направлена противоположно скорости
после удара о плиту направлена противоположно скорости 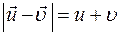 . Тогда численное значение силы взаимодействия
. Тогда численное значение силы взаимодействия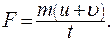 (1)
(1)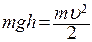 ,
,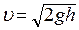 ,
,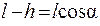
 ,
,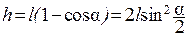 ,
,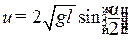 . (2)
. (2)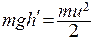 .
. . (3)
. (3)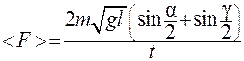 . (4)
. (4)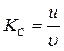 . (5)
. (5)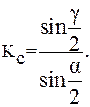 (6)
(6)


