Общие сведения. В воздухе, как и во всякой газообразной среде, могут распространяться только продольные волны
В воздухе, как и во всякой газообразной среде, могут распространяться только продольные волны. Поэтому звуковая волна в воздухе представляет собой чередование сжатий и разрежений. При сжатии увеличивается давление воздуха и, следовательно, возрастает его упругость. При разрeжении упругость воздуха уменьшается. Соответственно, при сжатии воздух нагревается, а при разрежении охлаждается. Эти изменения температуры приводят к добавочному изменению упругости воздуха (возрастание и уменьшение соответственно). Такие изменения температуры, вызывающие добавочное изменение упругости воздуха, возникают лишь тогда, когда сжатия и разрежение воздуха быстро сменяют друг друга, т.е. когда соседние участки воздуха не успевают обмениваться теплотой и процесс сжатия и разрежения воздуха близок к адиабатическому. Лаплас впервые доказал, что сжатия и разрежения в звуковой волне в воздухе происходят адиабатически и скорость звука в воздухе увеличивается благодаря изменениям температуры, производимым самой звуковой волной. Эти изменения температуры невелики и не влияют на среднюю температуру воздуха. Определим скорость распространения звука в воздухе, считая его сплошной однородной упругой средой, плотность которой равна ρ. В этой среде мысленно выделим некоторый цилиндрический объем с плoщaдъю поперечного сечения S.
Этому уплотнению соответствует масса:
и импульс:
где
скорость распространения импульса деформации сжатия. Можно полагать, что такой импульс будет соответствовать уплотнению во втором и последующих слоях воздуха (среда однородная). Приравняем этот импульс к импульсу внешней силы:
где dt - промежуток времени, в течение которого деформация сжатия охватывает слой dx. Изменение давления при деформации:
Отсюда скорость распространения звуковой волны:
T.е. скорость распространения звука определяется отношением изменения давления к изменению плотности в любой, сплошной, однородной и упругой среде. В дифференциальной форме :
При адиабатическом процессе объем и давление газа связаны уравнением Пуассона:
где
отношение теплоемкости газа при постоянном давлении к теплоемкости при постоянном объеме. Поскольку плотность газа обратно пропорциональна его объему, то:
Дифференцируя это выражение, получим
Отсюда:
Следовательно:
Это формула Лапласа. Хотя в последнюю формулу входит давление P, скорость звука от давления не зависит, т.к изменениe давления пропорционально изменению плотности воздуха. Скорость звука в воздухе зависит от температуры. Установим эту зависимость, воспользовавшись формулой Клапейрона-Менделеева для одного моля газа (воздуха):
PV=RT. Из этой формулы:
Следовательно,
т.к
где m- молярная масса воздуха. Из этой формулы:
Формула (10) является расчетной. Чтобы вычислить gпо этой формуле необходимо вначале определить скорость звука в воздухе. Для определения скорости звука в воздухе в этой работе используется метод стоячей волны. Процесс распространения колебаний в упругой среде называется волной. Расстояние, на которое распространяется волна за время, равное периоду колебания, называется длиной волны. Длина волны связана с периодом колебания частиц T и скоростью распространения волны u соотношением:
где
Рассмотрим стоячие волны, которые образуются в трубе с воздухом длиной Это условие выполняется, если в трубе укладывается половина длины бегущей волны:
где k=1, 2, 3.... Выразив l из (1) и подставив в формулу:
получим:
Полученная формула (13) выражает собственные частоты колебаний воздушного столба в трубе длиной
|

 Пусть кратковременный импульс силы F (на рис. 1 показан стрелками), равномерно распределенной по сечению S, вызывает смещение вправо частиц среды (воздуха) в узком слое, прилегающему к этому сечению. Вследствие инертности, соседний к нему слой окажется деформированным и в нем возникнут упругие силы, стремящиеся остановить частицы первого слоя и привести в движение частицы второго слоя. В итоге действие упругих сил приведет к исчезновению деформации сжатия в этом слое и к ее возникновению в следующем слое. Таким образом, импульс деформации сжатия передается от слоя к слою с некоторой скоростью
Пусть кратковременный импульс силы F (на рис. 1 показан стрелками), равномерно распределенной по сечению S, вызывает смещение вправо частиц среды (воздуха) в узком слое, прилегающему к этому сечению. Вследствие инертности, соседний к нему слой окажется деформированным и в нем возникнут упругие силы, стремящиеся остановить частицы первого слоя и привести в движение частицы второго слоя. В итоге действие упругих сил приведет к исчезновению деформации сжатия в этом слое и к ее возникновению в следующем слое. Таким образом, импульс деформации сжатия передается от слоя к слою с некоторой скоростью 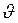 , отличной от скорости смещающихся частиц воздуха. Пусть в начале деформация сжатия, охватывает слой воздуха толщиной dx, а средняя плотность среды в нем возрастает до
, отличной от скорости смещающихся частиц воздуха. Пусть в начале деформация сжатия, охватывает слой воздуха толщиной dx, а средняя плотность среды в нем возрастает до 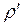 .
. 
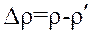 . (1)
. (1)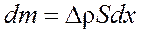 , (2)
, (2)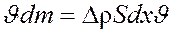 , (3)
, (3) , (4)
, (4)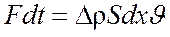 , (5)
, (5)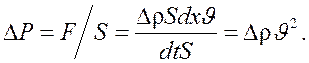 (6)
(6)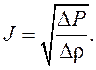
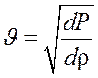 . (7)
. (7)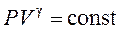 ,
,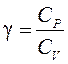 ,
,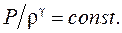 .
.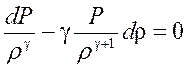 .
.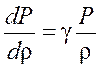 .
.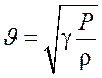 . (8)
. (8)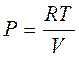 .
.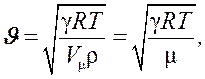 (9)
(9)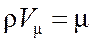 ,
,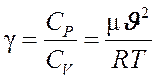 . (10)
. (10)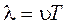 , или
, или 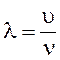 , (11)
, (11)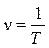 - частота колебания частиц среды.
- частота колебания частиц среды. Если две волны одинаковой частоты и амплитуды распространяются навстречу друг другу, то в результате их наложения при определенных условиях может возникнуть стоячая волна. В среде, где установились стоячие волны, колебания частиц происходят с различной амплитудой. В определенных точках среды амплитуда колебания равна нулю, эти точки называются узлами; в других точках амплитуда равна сумме амплитуд складываемых колебаний, такие точки называются пучностями. Расстояние между двумя соседними узлами (или пучностями) равно l/2, где l - длина бегущей волны (рис. 2). Стоячая волна может образоваться при наложении падающей и отраженной волн. При этом, если отражение происходит от среды во много раз более плотной, чем среда, в которой распространяется волна, то в месте отражения смещение частиц равно нулю, то есть образуется узел. Если волна отражается от среды менее плотной, то из-за слабого задерживающего действия частиц второй cреды на границе возникают колебания с удвоенной амплитудой, то есть образуется пучность. В том случае, когда плотности сред мало отличаются друг от друга, наблюдается частичное отражение волн от границы раздела двух сред.
Если две волны одинаковой частоты и амплитуды распространяются навстречу друг другу, то в результате их наложения при определенных условиях может возникнуть стоячая волна. В среде, где установились стоячие волны, колебания частиц происходят с различной амплитудой. В определенных точках среды амплитуда колебания равна нулю, эти точки называются узлами; в других точках амплитуда равна сумме амплитуд складываемых колебаний, такие точки называются пучностями. Расстояние между двумя соседними узлами (или пучностями) равно l/2, где l - длина бегущей волны (рис. 2). Стоячая волна может образоваться при наложении падающей и отраженной волн. При этом, если отражение происходит от среды во много раз более плотной, чем среда, в которой распространяется волна, то в месте отражения смещение частиц равно нулю, то есть образуется узел. Если волна отражается от среды менее плотной, то из-за слабого задерживающего действия частиц второй cреды на границе возникают колебания с удвоенной амплитудой, то есть образуется пучность. В том случае, когда плотности сред мало отличаются друг от друга, наблюдается частичное отражение волн от границы раздела двух сред.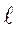 , закрытой с двух сторон (рис. 2а). Через небольшое отверстие в одном конце трубы при помощи динамика возбудим колебания звуковой частоты. Тогда в воздухе внутри трубы распространится звуковая волна, которая отразится от другого закрытого конца и побежит обратно. Казалось бы, что должна возникнуть стоячая волна при любой частоте колебаний. Однако, в трубе, закрытой с двух сторон, на концах должны образовываться узлы.
, закрытой с двух сторон (рис. 2а). Через небольшое отверстие в одном конце трубы при помощи динамика возбудим колебания звуковой частоты. Тогда в воздухе внутри трубы распространится звуковая волна, которая отразится от другого закрытого конца и побежит обратно. Казалось бы, что должна возникнуть стоячая волна при любой частоте колебаний. Однако, в трубе, закрытой с двух сторон, на концах должны образовываться узлы. =l/2 (рис. 2б). Здесь амплитуды смещения частиц воздуха отложены по вертикали. Сплошной линией изображена бегущая волна, пунктиром - отраженная. В трубе возможна и такая стоячая волна, где имеется и еще один узел, при этом укладываются две половины длины волны:
=l/2 (рис. 2б). Здесь амплитуды смещения частиц воздуха отложены по вертикали. Сплошной линией изображена бегущая волна, пунктиром - отраженная. В трубе возможна и такая стоячая волна, где имеется и еще один узел, при этом укладываются две половины длины волны: 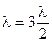 . Таким образом, в трубе, закрытой с двух сторон, стоячая волна образуется в тех случаях, когда на длине трубы укладывается целое число половин длин волн:
. Таким образом, в трубе, закрытой с двух сторон, стоячая волна образуется в тех случаях, когда на длине трубы укладывается целое число половин длин волн: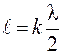 , (12)
, (12)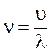 ,
,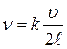 . (13)
. (13)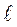 , где k =1 соответствует основному тону, k =1,2,3... - обертонам. В общем случае колебание столба воздуха может быть представлено как наложение собственных колебаний.
, где k =1 соответствует основному тону, k =1,2,3... - обертонам. В общем случае колебание столба воздуха может быть представлено как наложение собственных колебаний.


