Краткие теоретические сведения. Свободные поверхности жидкостей находятся в особом состоянии натяжения
Свободные поверхности жидкостей находятся в особом состоянии натяжения. Силы поверхностного натяжения направлены по касательной к поверхности жидкости и действуют нормально к любой линии, мысленно проведенной на этой поверхности. Для количественной характеристики силы поверхностного натяжения вводят коэффициент поверхностного натяжения - s, который равен силе, отнесенной к единице длины:
Наличие сил поверхностного натяжения можно понять из следующих рассуждений. Поверхность жидкости, соприкасающаяся с ее паром или другой средой (воздухом), находится в особых условиях, т.к. молекулы поверхностного слоя взаимодействуют с молекулами двух сред, имеющих различную плотность. Последнее обстоятельство обусловливает равнодействующую сил:
действующих на молекулу в поверхностном слое, направленную внутрь жидкости (рис.1). Таким образом, у поверхности жидкости будут действовать силы, образующие “поверхностное” силовое поле, расположенное в тонком слое порядка нескольких межмолекулярных расстояний в жидкостях. Молекулы, находящиеся в этом поле, обладают повышенной потенциальной энергией. Следовательно, при выходе молекул из глубины жидкости на поверхность их потенциальная энергия возрастает. Изменения энергии происходит в поверхностном слое (пленке) толщиной 10-7 cм. При изменении формы поверхности жидкости или изменении ее площади часть молекул с повышенной энергией уходят внутрь жидкости, освобождающаяся при этом энергия расходуется на увеличение теплового движения молекул.
Кроме силового смысла, который определяется из выражения (1), коэффициент поверхностного натяжения имеет и энергетический смысл. Для понятия этого смысла рассмотрим случай, когда жидкость существует в форме тонкой пленки, примером которой может служить мыльная пленка. Возьмем проволочный каркас, имеющий форму прямоугольника, рис.2.
A=2FDx. (2)
Площадь поверхности пленки увеличится на
Из выражения (3) следует, что коэффициент поверхностного натяжения равен работе, затраченной на увеличение поверхности пленки на единицу площади. В этом заключается энергетический смысл s. Вследствие действия сил поверхностного натяжения искривленный поверхностный слой производит на жидкость давление DP, дополнительное к внешнему давлению и обусловленное кривизной поверхности. Определим величину дополнительного давления для случая, когда поверхность жидкости представляет собой часть сферы радиусом R. Отсечем мысленно малый сферический сегмент DS, рис.3. Силы поверхностного натяжения, приложенные к контуру этого сег
DFi=sD
Разложим силу Величина равнодействующей силы будет равна алгебраической сумме сил
Заменив в последнем выражении DFi соотношением (4) и cosj отношением r к R, получим:
так как Давление DP получим, поделив значение силы F на площадь, ограниченную контуром, т.е.:
Формула (5) дает величину добавочного давления, оказываемого на жидкость со стороны сферической поверхности, и всегда направленного к центру кривизны поверхности.
В случае вогнутой поверхности давление отрицательно, так как направлено не внутрь жидкости, а наружу, и давление на жидкость будет меньше внешнего. В данной работе формула (5) использована для определения s.
|

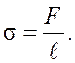 (1)
(1) ,
, Поэтому при отсутствии внешних сил или при их незначительности поверхность жидкости будет сокращаться и жидкость примет форму с минимальной поверхностью, возможной в данных условиях. Например, в поле силы тяжести капли жидкости с уменьшением их размера приближаются к сферической форме из-за незначительности веса капли.
Поэтому при отсутствии внешних сил или при их незначительности поверхность жидкости будет сокращаться и жидкость примет форму с минимальной поверхностью, возможной в данных условиях. Например, в поле силы тяжести капли жидкости с уменьшением их размера приближаются к сферической форме из-за незначительности веса капли. Сторона может свободно скользить вдоль направляющих АС и ВД, затянем площадь АВСД мыльной пленкой. Пленка эта двойная, подобно листу бумаги. Опыт показывает, что пленка стремиться сократиться и перемычка СД приходит в движение вверх. Для удержания в равновесии перемычки СД к ней надо приложить определенную силу, например, подвесить грузик, Так как пленка двойная, то величину этой силы обозначим 2
Сторона может свободно скользить вдоль направляющих АС и ВД, затянем площадь АВСД мыльной пленкой. Пленка эта двойная, подобно листу бумаги. Опыт показывает, что пленка стремиться сократиться и перемычка СД приходит в движение вверх. Для удержания в равновесии перемычки СД к ней надо приложить определенную силу, например, подвесить грузик, Так как пленка двойная, то величину этой силы обозначим 2  , считая, что на каждую сторону пленки действует сила
, считая, что на каждую сторону пленки действует сила 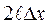 = 2DS, где
= 2DS, где  - длина перемычки СД, DS - увеличение поверхности каждой стороны пленки. С учетом (1) формулу (2) можно записать: A=
- длина перемычки СД, DS - увеличение поверхности каждой стороны пленки. С учетом (1) формулу (2) можно записать: A= 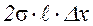 =2sDS, или окончательно:
=2sDS, или окончательно: . (3)
. (3) мента, касательные к сферической поверхности. На элемент контура
мента, касательные к сферической поверхности. На элемент контура 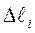 действует сила:
действует сила: . (4)
. (4)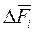 , на составляющие
, на составляющие 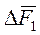 , и
, и  . Геометрическая сумма сил D
. Геометрическая сумма сил D 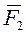 , приложенных ко всему контуру, равна нулю. Поэтому равнодействующая
, приложенных ко всему контуру, равна нулю. Поэтому равнодействующая  :
: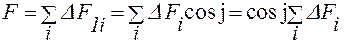 .
.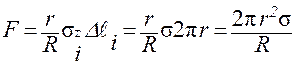 ,
,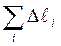 равна длине окружности радиуса r.
равна длине окружности радиуса r. . (5)
. (5) Если поверхность жидкости выпукла, то давление на жидкость больше внешнего давления на величину DP, рис. 4.
Если поверхность жидкости выпукла, то давление на жидкость больше внешнего давления на величину DP, рис. 4.


