VI. Коэффициент напряженности работы
Сложность сетевого графика оценивается коэффициентом сложности Ксл=17/10=1,7. Сетевые графики, имеющие коэффициент сложности 1,7 являются графиками средней сложности. Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициента напряженности работ. В результате расчетов следует, что: - работы таблицы 6 входят в критическую зону (Kн(i,j)>0,8) Таблица 6 – Расчет коэффициентов напряженности работ
- работы, входящие в подкритическую зону (0,6≤ Kн(i,j)≤ 0,8) отсутствуют. - работы таблицы 7 входят в резервную зону (Kн(i,j)<0,6)
Таблица 7 – Расчет коэффициентов напряженности работ
По результатам нахождения коэффициентов напряженности видно, что большинство работ близки к 1, следовательно, тем сложнее выполнить данные работы в установленные сроки. Необходимо перераспределить требуемые ресурсы из менее напряженных зон в данные. Необходимо также передать часть критических работ на остальные пути, имеющие резервы времени. Лишь несколько работ близки к 0, то есть большим относительным резервом обладает максимальный путь, проходящий через данные работы
VI. Сетевое планирование в условиях неопределенности
Рассмотрим сетевой график в условиях неопределенности. При этом оценим вероятность выполнения проекта в срок Т = 42 сутки. Математическое ожидание и дисперсии работ рассчитаны в таблице 8.
Вероятность того, что весь комплекс работ будет выполнен не более чем за 42 суток, составляет 89,9%. Таблица 8 – Расчет числовых характеристик случайной величины
Найдем решение обратной задачи: оценить максимально возможный срок Т выполнения проекта с надежностью β =0,95.
Ф(1,96)=0,95 Т=33,67+Z0.95×2,29=33,67+1,96×2,29=38,1584≈38 Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95 % составляет всего 38 суток. Выводы В результате проведенного сетевого планирования некоторого проекта были получены следующие результаты: - Рассчитаны все полные пути, в том числе критический. Продолжительность критического пути составляет 31, то есть для проведения комплекса работ понадобиться 31 сутки. - Найдены временные характеристики графа. - В результате оптимизации сетевого графа, не меняя продолжительность выполнения всего проекта, увеличили продолжительность некоторых работ (0,3), (0,7), (1,4), (2,8), (3,5), (3,6), (4,7), (4,8), (5,8), (7,9) на величину - В результате расчетов найдены коэффициенты напряженности для определения сложности исполнения намеченных работ в срок. Для выравнивания трудоемкости критических работ необходимо осуществить передачу части работ на пути, имеющие резервы времени и перераспределить ресурсы из зон менее напряженных в критическую. - Проект рассмотрен в условиях неопределенности. Рассчитаны средние характеристики работ. На их основе была найдена вероятность того, что весь комплекс работ будет выполнен не более чем за 42 сутки, составляет 89,9%. Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95 % составляет 38 суток.
|

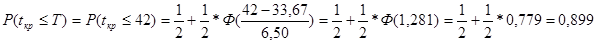
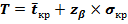
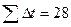 и уменьшили стоимость всего проекта на величину равную,
и уменьшили стоимость всего проекта на величину равную, 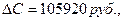 то есть на 19,58%.
то есть на 19,58%.


