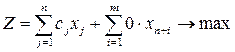Взаимосвязь однородной и канонической форм записиОбщая ЗЛП может быть с помощью эквивалентных преобразований приведена сначала к однородной, а затем к канонической форме. Рассмотрим этот процесс более подробно. Перевод общей ЗЛП в однородную форму. Основным отличием общей формы от однородной является наличие в составе ограничений некоторого количества уравнений вида (7); каждое такое уравнение
Эквивалентные преобразования однородной модели в каноническую. 1. Каждое исходное неравенство типа «меньше или равно» приводится к эквивалентной системе из уравнения и тривиального неравенства добавлением своей балансовой переменной:
2. Каждое исходное неравенство типа «больше или равно» приводится к эквивалентной системе из уравнения и тривиального неравенства вычитанием своей балансовой переменной:
Поскольку новые переменные вводятся от каждого неравенства, размерность задачи возрастает. 3. Если на какую-нибудь переменную не наложено условие неотрицательности, её можно представить как разность двух неотрицательных переменных:
4. Если 5. Дополнительные балансовые переменные
|
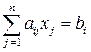эквивалентно системе из двух нестрогих неравенств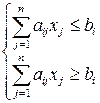 
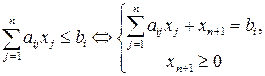(xn+1 – балансовая переменная)
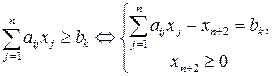, (xn+2 – балансовая переменная)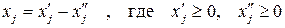
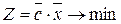, то это требование эквивалентно требованию 
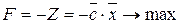, то есть при необходимости задачу минимизации можно заменить задачей максимизации и наоборот.
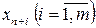вводятся в целевую функцию с коэффициентами, равными нулю: 
