Преобразование канонической модели в симплексную. Основная идея симплекс-метода
Рассмотрим ЗЛП в канонической форме записи:
Для определенности будем считать, что число неизвестных больше числа уравнений, то есть Напомним некоторые сведения из теории систем линейных алгебраических уравнений. В системе (1) все переменные можно разделить на две группы: базисные (основные) и свободные (неосновные). Базисные переменные- это любые n переменных, определитель из коэффициентов которых в системе (1) не равен нулю. Остальные переменные в этой системе являются свободными. Естественно, выбор базиса в такой системе не является единственным. Решение системы (1) называется допустимым, если при этом выполняются ограничения (2), то есть все компоненты вектора решения неотрицательны. Решение системы (1) называется базисным, если в нем все свободные переменные равны нулю. Допустимое базисное решение называется опорнымпланом. Эквивалентными Гауссовыми преобразованиями всякая каноническая форма приводится к симплексной форме, позволяющей получить исходное опорное решение:
В системе (4) переменные
Если в системе ограничений (4) все свободные члены сохранили свою неотрицательность, то задача в форме (4)-(5) называется симплексной моделью ЗЛП. следует отметить, что единого метода получения симплексной модели в форме (4)-(5) не существует. Во многих случаях прийти к такой записи невозможно, и приходится применять искусственные приёмы. Однако здесь будем считать, что нам такую запись получить удалось. Обнулим в системе (4) все свободные переменные, получим базисное решение в виде Чтобы удовлетворить неравенствам (2) и получить допустимое решение, надо выполнить преобразования Гаусса так, чтобы все свободные члены остались неотрицательными. Поэтому алгоритм Гаусса требует некоторого уточнения, и для этого приведем некоторые дополнительные сведения. Определение. Если в системе уравнений (1) все свободные члены неотрицательны, то допустимым отношением к выбранному k - му ключевому столбцу называется число
в противном случае Теорема (о допустимых отношениях). Если в любой очередной итерации гауссовых преобразований системы (1) с При подготовке очередной итерации преобразования матрицы системы по методу Гаусса нужно выбрать элемент, который будет превращен в единицу, а остальные элементы этого же столбца обнуляются. В классическом методе Гаусса роль такого элемента выполняет один из диагональных элементов матрицы. В симплекс-методе в роли такого элемента выступает ведущий элемент, полученный с помощью выбора минимального допустимого отношения. Очень важной для понимания смысла решения ЗЛП является следующее утверждение. Теорема. Опорное решение задачи (1)-(3) и угловая точка ОДР этой задачи эквивалентны. Отсюда следует, что на каждой итерации мы получаем опорный план, который по своему геометрическому смыслу является одной из угловых точек ОДР задачи. Теорема. (Достаточное условие оптимальности опорного решения) Если в симплексной модели ЗЛП в целевой функции (5) все коэффициенты при свободных переменных Теперь сформулируем главную идею симплекс-метода: Найти исходное опорное решение ЗЛП (то есть угловую точку ОДР). Модифицированными гауссовыми преобразованиями поэтапно улучшать решение до получения оптимального варианта, если он существует. Поэтапный процесс конечен, так как конечно число угловых точек. Если ОДР не ограничена, то алгоритм симплекс-метода также достаточно быстро определяет это.
|

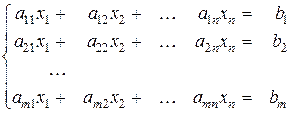
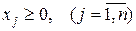
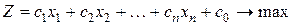
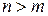 . Это обычная ситуация для экономических задач, поскольку каноническая форма получается из однородной преобразованием неравенств в уравнения, и при этом размерность задачи (определяемая числом переменных) возрастает и становится больше числа ограничений. Кроме этого, без потери общности будем считать все свободные члены нетривиальных ограничений (1) неотрицательными. В противном случае можно соответствующее уравнение умножить на (-1). Обратите также внимание на наличие свободного члена в целевой функции (3), который обычно появляется в ней в случае замены переменных.
. Это обычная ситуация для экономических задач, поскольку каноническая форма получается из однородной преобразованием неравенств в уравнения, и при этом размерность задачи (определяемая числом переменных) возрастает и становится больше числа ограничений. Кроме этого, без потери общности будем считать все свободные члены нетривиальных ограничений (1) неотрицательными. В противном случае можно соответствующее уравнение умножить на (-1). Обратите также внимание на наличие свободного члена в целевой функции (3), который обычно появляется в ней в случае замены переменных.
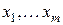 являются базисными, а переменные
являются базисными, а переменные  - свободными. Из системы (4) можно получить выражения всех базисных переменных через свободные. После подстановки этих выражений в целевую функцию (3) получим функцию, в которой отсутствуют базисные переменные:
- свободными. Из системы (4) можно получить выражения всех базисных переменных через свободные. После подстановки этих выражений в целевую функцию (3) получим функцию, в которой отсутствуют базисные переменные: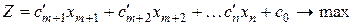
 . Другому набору базисных переменных будет соответствовать и другая симплексная форма данной задачи. Решение исходной оптимизационной задачи заключается в нахождении такого сочетания базисных переменных, которому отвечает максимальное значение целевой функции (5).
. Другому набору базисных переменных будет соответствовать и другая симплексная форма данной задачи. Решение исходной оптимизационной задачи заключается в нахождении такого сочетания базисных переменных, которому отвечает максимальное значение целевой функции (5).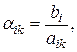 если aik>0
если aik>0 
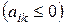 это отношение не существует или не является допустимым.
это отношение не существует или не является допустимым.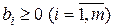 в качестве ключевого выбран k -й столбец, то выбор в нем ключевого элемента в строке, соответствующей минимальному допустимому отношению, гарантирует сохранение неотрицательности всех свободных членов в результате очередной итерации.
в качестве ключевого выбран k -й столбец, то выбор в нем ключевого элемента в строке, соответствующей минимальному допустимому отношению, гарантирует сохранение неотрицательности всех свободных членов в результате очередной итерации.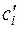 неположительны, то соответствующее этой форме опорное решение оптимально.
неположительны, то соответствующее этой форме опорное решение оптимально.


