Вернемся к нашему примеру ЗЛП:
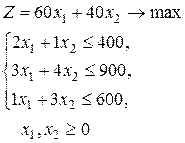
Эта задача в двойственной форме имеет вид:
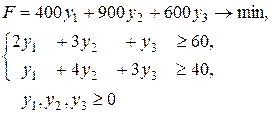
Исходная задача была нами решена графически, и решение равно  . Воспользуемся теоремой о дополняющей нежесткости и подставим компоненты этого решения в ограничения исходной задачи. В результате видно, что первое и второе ограничения выполняются как точные равенства, а третье ограничение является строгим неравенством. Согласно теореме, третья переменная двойственной задачи должна быть равна нулю, т.е.
. Воспользуемся теоремой о дополняющей нежесткости и подставим компоненты этого решения в ограничения исходной задачи. В результате видно, что первое и второе ограничения выполняются как точные равенства, а третье ограничение является строгим неравенством. Согласно теореме, третья переменная двойственной задачи должна быть равна нулю, т.е.  . Согласно этой же теореме, поскольку обе компоненты решения исходной задачи не равны нулю, и оба ограничения двойственной задачи выполняются как равенства. Если в этих равенствах обнулить последнюю переменную, то получим систему двух уравнений с двумя неизвестными:
. Согласно этой же теореме, поскольку обе компоненты решения исходной задачи не равны нулю, и оба ограничения двойственной задачи выполняются как равенства. Если в этих равенствах обнулить последнюю переменную, то получим систему двух уравнений с двумя неизвестными:
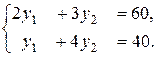
Решая эту систему, получаем  .
.
Другим способом получения двойственного решения является использование симплекс-таблиц исходной задачи. Рассмотрим последюю симплекс-таблицу из предыдущего раздела. Решение двойственной задачи (план) находится в индексной строке, в столбцах, соответствующих первоначальному базису.
Рассмотрим данный способ в более общей постановке. Пусть имеется пара двойственных задач, основная и двойственная. Предположим, что с помощью симплекс-метода найден оптимальный план  прямой задачи, и этот план определяется базисом, образованным векторами
прямой задачи, и этот план определяется базисом, образованным векторами  . Обозначим через
. Обозначим через  матрицу-строку, составленную из коэффициентов при этих переменных в целевой функции прямой задачи, а через
матрицу-строку, составленную из коэффициентов при этих переменных в целевой функции прямой задачи, а через 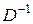 - матрицу, обратную матрице D, составленной из компонент векторов оптимального базиса. Тогда имеет место следующее утверждение.
- матрицу, обратную матрице D, составленной из компонент векторов оптимального базиса. Тогда имеет место следующее утверждение.
Теорема. Если основная задача линейного программирования имеет оптимальный план  , то
, то 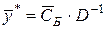 является оптимальным планом двойственной задачи.
является оптимальным планом двойственной задачи.
Применительно к рассмотренному нами примеру матрица D, составленная из столбцов первоначальной симплекс-таблицы, соответствующих окончательномубазису, имеет вид:
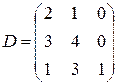 . Тогда обратная к ней матрица равна
. Тогда обратная к ней матрица равна 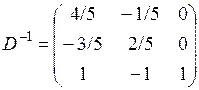 . Вектор
. Вектор  находится в левой части последней симплекс-таблицы и равен
находится в левой части последней симплекс-таблицы и равен 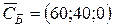 . Проведем перемножение, получим результат:
. Проведем перемножение, получим результат:
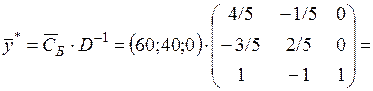
 . Эти значения и находятся в индексной строке последней таблицы.
. Эти значения и находятся в индексной строке последней таблицы.

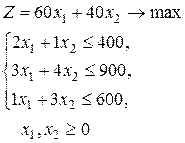
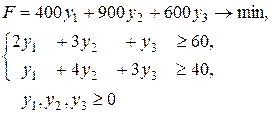
 . Воспользуемся теоремой о дополняющей нежесткости и подставим компоненты этого решения в ограничения исходной задачи. В результате видно, что первое и второе ограничения выполняются как точные равенства, а третье ограничение является строгим неравенством. Согласно теореме, третья переменная двойственной задачи должна быть равна нулю, т.е.
. Воспользуемся теоремой о дополняющей нежесткости и подставим компоненты этого решения в ограничения исходной задачи. В результате видно, что первое и второе ограничения выполняются как точные равенства, а третье ограничение является строгим неравенством. Согласно теореме, третья переменная двойственной задачи должна быть равна нулю, т.е.  . Согласно этой же теореме, поскольку обе компоненты решения исходной задачи не равны нулю, и оба ограничения двойственной задачи выполняются как равенства. Если в этих равенствах обнулить последнюю переменную, то получим систему двух уравнений с двумя неизвестными:
. Согласно этой же теореме, поскольку обе компоненты решения исходной задачи не равны нулю, и оба ограничения двойственной задачи выполняются как равенства. Если в этих равенствах обнулить последнюю переменную, то получим систему двух уравнений с двумя неизвестными: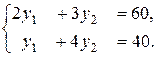
 .
. прямой задачи, и этот план определяется базисом, образованным векторами
прямой задачи, и этот план определяется базисом, образованным векторами  . Обозначим через
. Обозначим через  матрицу-строку, составленную из коэффициентов при этих переменных в целевой функции прямой задачи, а через
матрицу-строку, составленную из коэффициентов при этих переменных в целевой функции прямой задачи, а через 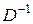 - матрицу, обратную матрице D, составленной из компонент векторов оптимального базиса. Тогда имеет место следующее утверждение.
- матрицу, обратную матрице D, составленной из компонент векторов оптимального базиса. Тогда имеет место следующее утверждение.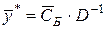 является оптимальным планом двойственной задачи.
является оптимальным планом двойственной задачи.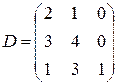 . Тогда обратная к ней матрица равна
. Тогда обратная к ней матрица равна 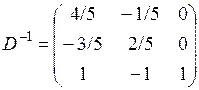 . Вектор
. Вектор  находится в левой части последней симплекс-таблицы и равен
находится в левой части последней симплекс-таблицы и равен 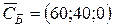 . Проведем перемножение, получим результат:
. Проведем перемножение, получим результат: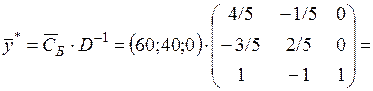
 . Эти значения и находятся в индексной строке последней таблицы.
. Эти значения и находятся в индексной строке последней таблицы.


