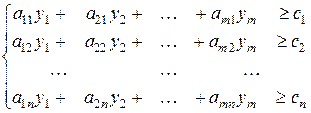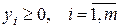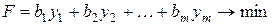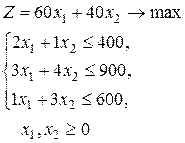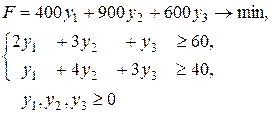Построение двойственной ЗЛП
Рассмотрим прямую задачу планирования производства (об использовании ресурсов): найти вектор
который обеспечивает максимум целевой функции
Пусть теперь на предприятии решили рассмотреть другой вариант извлечения прибыли не через производство и продажу готовых изделий, а путем продажи имеющихся запасов сырья. Возникает новая задача, называемая двойственной: какова должна быть цена единицы каждого из ресурсов Цель продавца здесь: выручка за сырьё, идущее на производство единицы продукции каждого вида, должна быть не меньше цены единицы этой продукции (иначе выгоднее самому организовать производство). Рассмотрим себестоимость единицы продукции первого вида в этих учетных ценах. Стоимость ресурса первого вида в этой продукции равна
Ограничения на переменные традиционны (поскольку цены на ресурсы не могут быть отрицательными):
Целью покупателя является минимизация затрат на приобретение ресурсов:
Итак, задача (4)-(6) – двойственная к задаче (1)-(3). Получили пару симметричных двойственных задач.
Общие правила составления двойственной задачи такие: 1. Матрица системы ограничений транспонируется. 2. Ограничения вида «меньше или равно» заменяются на ограничения «больше или равно». 3. Свободные члены исходной задачи становятся коэффициентами целевой функции задачи двойственной. 4. Коэффициенты целевой функции исходной задачи становятся свободными членами двойственной. 5. Исходная задача на максимум преобразуется в двойственную к ней на минимум. Пример. Составить двойственную задачу к ранее рассмотренной:
Двойственная задача будет записана в такой форме:
|

 при ограничениях
при ограничениях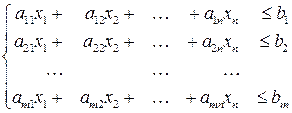
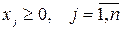
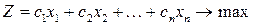
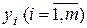 , чтобы эта продажа имела смысл? Таким образом, нужно найти вектор цен
, чтобы эта продажа имела смысл? Таким образом, нужно найти вектор цен  .
.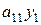 , стоимость ресурса второго вида равна
, стоимость ресурса второго вида равна 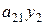 , и т.д., стоимость m -го ресурса в первом изделии составляет
, и т.д., стоимость m -го ресурса в первом изделии составляет 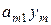 . Просуммируем эти величины, получим себестоимость первого изделия, которая должна быть не меньше цены реализации этого изделия С1.. Аналогичные неравенства составим и для всех остальных видов продукции, получаем ограничения двойственной задачи:
. Просуммируем эти величины, получим себестоимость первого изделия, которая должна быть не меньше цены реализации этого изделия С1.. Аналогичные неравенства составим и для всех остальных видов продукции, получаем ограничения двойственной задачи: