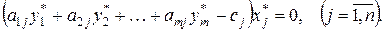Исследование пары двойственных задач
Поскольку двойственная задача также является ЗЛП, то её можно решить симплекс-методом. Однако двойственная задача и экономически, и математически тесно связана с прямой задачей, поэтому есть более простые способы её решения, если известно решение прямой задачи. Поэтому рассмотрим некоторые результаты, связывающие обе эти задачи. Теорема. Пусть
Теорема (достаточный признак оптимальности пары двойственных ЗЛП, или критерий оптимальности Канторовича). Если Первая теорема двойственности. Если одна из двойственных задач имеет оптимальное решение, то и другая задача также имеет оптимальное решение, причем
Экономической интерпретацией этой теоремы является утверждение, что при оптимальном плане суммарная стоимость запасов сырья равна суммарной стоимости продукции. Вторая теорема двойственности (теорема о дополняющей нежесткости). Оптимальные решения
Формулы (9) и (10) можно применять следующим образом: - если при оптимальном решении одной из пары двойственных задач какое-либо неравенство выполняется как строгое, то соответствующая ему двойственная переменная в оптимальном решении другой задачи равна нулю; - если какая-нибудь переменная в оптимальном решении одной из задач не равна нулю, то соответствующее ей ограничение другой задачи выполняется как равенство.
|
есть допустимоерешение задачи (1)-(3), 
есть допустимоерешение задачи (4)-(6). Тогда выполняется неравенство:
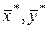- такие допустимые решения (1)-(3) и (4)-(6) соответственно, что 
, то 
