Экономическая интерпретация двойственных оценок
Согласно первой теореме двойственности,
т.е. доход зависит от объёмов ресурсов:
Сделаем следующие выводы: Формула (11) отражает общий принцип баланса результатов производства Из (11) и (12) следует, что
Например, увеличение избыточного ресурса не оказывает влияния на прибыль Двойственные оценки определяют дефицитные Замечание. Формула (13) верна только при достаточно малом изменении объёмов ресурсов по сравнению с их общим количеством. Если это изменение велико, то учетная цена того или иного ресурса может стать нулевой. Точные количественные границы такого изменения рассмотрим ниже.
|
, следовательно, можем записать:
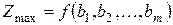. Вычислим градиент этой функции:
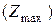и затрат 
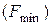. Двойственные оценки обеспечивают этот баланс.
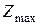при изменении отдельно взятого ресурса на единицу увеличивается ровно на величину двойственной оценки этого ресурса: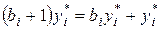
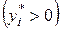и избыточные 
ресурсы. Например, в ранее рассмотренном примере из решения симплекс-методом видно, что третий ресурс является избыточным при производстве продукции, поскольку 
. Это подтверждается также и тем фактом, что значение балансовой переменной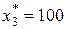 
, и это означает неиспользованный остаток сырья третьего вида.
