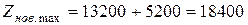Устойчивость двойственных оценокДвойственные оценки Теорема. При изменении объёма ресурсов двойственные оценки будут устойчивыми, если выполняется неравенство:
В формуле (14) вектор
Таким образом, при данном изменении объёмов ресурсов двойственные оценки не изменятся (будут устойчивыми). Новое значение целевой функции при измененных ресурсах можно определить по выражению:
Значение
Применяя результаты нашего примера, получим
Выражение (14) можно также использовать для определения границ устойчивости двойственных оценок по ресурсам. Однако неравенство (14) представляет собой многогранник в многомерном пространстве, и совместное решение довольно сложно. Поэтому целесообразно решать эти неравенства по каждому из ресурсов отдельно, принимая все остальные ресурсы неизменными.
|
при некотором изменении запасов ресурсов 
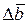называются устойчивыми, если при решении измененной ЗЛП эти двойственные оценки не изменяются. Разумеется, обеспечить устойчивость двойственных оценок можно только в определенных границах. Эти границы определяются следующей теоремой.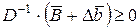
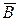означает первоначальный объём ресурсов. Матрица 
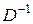составлена, как уже указывалось выше, из столбцов последней симплекс-таблицы, соответствующих первоначальному базису. Например, если изменить запасы ресурсов в ранее рассмотренной задаче на величину 
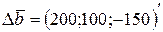(штрих означает транспонирование, а знак минус уменьшение объёма третьего ресурса), то можно проверить условие устойчивости так:
.
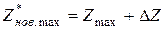находим с использованием первой теоремы двойственности: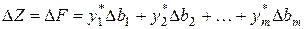
.
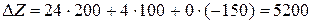. Отсюда 
