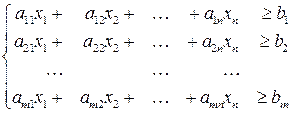Экономико-математические модели задач ЛП
ЭММ планирования производства (задача о наилучшем использовании ресурсов) Дано: - предприятие выпускает n различных видов продукции (j=1,2,…,n); - оно располагает для этого m видами ресурсов (i=1,2,…,m) (например, рабочая сила, площади, сырьё, энергия и пр.); - ресурсы ограничены и составляют - цена реализации j- го продукта равна - технологические коэффициенты aij: сколько единиц i- го ресурса расходуется для производства единицы j- го вида продукции. Найти план производства изделий Составим ЭММ данной задачи. Общий размер прибыли от реализации всей продукции равен сумме
Теперь составим баланс расхода по каждому ресурсу. Скажем, расход i- го ресурса складывается из затрат на производство 1-го изделия, то есть ai1x1, расхода на производство 2-го изделия ai2x2,…, расхода на производство n- го изделия ainxn. С другой стороны, этот суммарный расход не может превысить общего количества этого ресурса, то есть bi. Таким образом, запишем аналогичные ограничения для каждого из ресурсов, получим систему неравенств:
Чтобы план был реален, он должен состоять из неотрицательных компонент:
Запишем ЗЛП о наилучшем использовании ресурсов в компактном виде: найти
Задача о смесях (выбор диеты, составление кормового рациона, приготовление различных смесей) Рассмотрим на примере задачи о диете: получить кормовой рацион с заданными свойствами (содержанием питательных веществ) при наименьших затратах на исходные сырьевые материалы. Дано: - n видов исходных продуктов (сено, силос и пр. для животноводства); - они содержат m видов питательных веществ (белки, жиры, углеводы, соли и т.д); - для жизнедеятельности надо потреблять не менее bi единиц i -го питательного вещества; - cj – стоимость единицы исходного продукта j – го вида; - aij – содержание i- го питательного вещества в единице j- го вида корма. Составим ЭММ задачи. Обозначим через xj количества кормов j- го вида. Тогда суммарная стоимость всего набора кормосмесей
Теперь составим баланс по каждому питательному веществу в кормовом рационе. Для i- го питательного вещества: содержание i- го питательного вещества в кормосмеси первого вида равно ai1x1, в кормосмеси второго вида равно ai2x2,…, в кормосмеси n- го вида равно ainxn. Общее количество i- го питательного вещества должно быть не меньше, чем bi. Это задаёт вид неравенства, и в результате запишем систему ограничений для всех питательных веществ:
Эти ограничения, как обычно, дополняются тривиальными ограничениями из физических соображений (поскольку нельзя произвести кормосмеси в отрицательных количествах!):
|

 условных единиц;
условных единиц; , то есть задан вектор цен
, то есть задан вектор цен 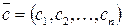 ;
;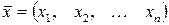 , обеспечивающий предприятию максимальную прибыль от реализации.
, обеспечивающий предприятию максимальную прибыль от реализации. . Таким образом, целевую функцию можно записать как максимум этого выражения
. Таким образом, целевую функцию можно записать как максимум этого выражения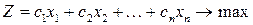

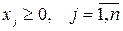
 при ограничениях
при ограничениях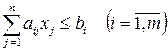 ;
;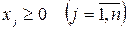 .
.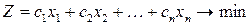 .
.