§ Неравенство Коши — Буняковского:
если принять в качестве скалярного произведения двух случайных величин ковариацию  , то норма случайной величины будет равна
, то норма случайной величины будет равна  , и следствием неравенства Коши — Буняковского будет:
, и следствием неравенства Коши — Буняковского будет:
 .
.
§ Коэффициент корреляции равен 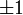 тогда и только тогда, когда
тогда и только тогда, когда 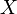 и
и  линейно зависимы (исключая события нулевой вероятности, когда несколько точек «выбиваются» из прямой, отражающей линейную зависимость случайных величин):
линейно зависимы (исключая события нулевой вероятности, когда несколько точек «выбиваются» из прямой, отражающей линейную зависимость случайных величин):
 ,
,
где  . Более того в этом случае знаки
. Более того в этом случае знаки  и
и  совпадают:
совпадают:
 .
.
Доказательство [показать]
§ Если  независимые случайные величины, то
независимые случайные величины, то  . Обратное в общем случае неверно.
. Обратное в общем случае неверно.
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными.

 , то норма случайной величины будет равна
, то норма случайной величины будет равна  , и следствием неравенства Коши — Буняковского будет:
, и следствием неравенства Коши — Буняковского будет: .
.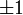 тогда и только тогда, когда
тогда и только тогда, когда 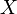 и
и  линейно зависимы (исключая события нулевой вероятности, когда несколько точек «выбиваются» из прямой, отражающей линейную зависимость случайных величин):
линейно зависимы (исключая события нулевой вероятности, когда несколько точек «выбиваются» из прямой, отражающей линейную зависимость случайных величин): ,
, . Более того в этом случае знаки
. Более того в этом случае знаки  и
и  совпадают:
совпадают: .
. независимые случайные величины, то
независимые случайные величины, то  . Обратное в общем случае неверно.
. Обратное в общем случае неверно.


