АВТОНОМНЫЙ ЗАТУХАЮЩИЙ ОСЦИЛЛЯТОР
Предположение, что груз на пружине не испытывает трения, приводит к выводу о незатухающем характере колебаний. Однако, из опыта известно, что если подождать достаточно долго, то амплитуда собственных колебаний груза постепенно уменьшается. Мы ошиблись, потому что исследовали не совсем верное уравнение. Теперь учтем силу трения. Будем считать, что она пропорциональна скорости движения груза. Тогда уравнение собственных колебаний груза будет таким:
или
где Известно, что решение уравнения (6) можно записать в виде:
где
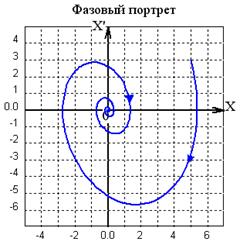
а) б) Рис.2 На рисунке 2а представлен график зависимости Такие затухающие колебания уже не являются гармоническими, так как их амплитуда уже не постоянна. Чем больше сила трения, тем быстрее затухают колебания. Так как колебания затухают по показательному закону, то теоретически они прекращаются только при Фазовые траектории в этом случае представляют собой скручивающиеся спирали. Они изображены на рис.2б.
|

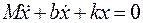 (5)
(5)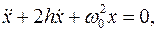 (6)
(6)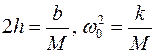 . Напомним, что
. Напомним, что 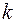 - коэффициент жесткости пружины,
- коэффициент жесткости пружины, 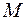 - масса груза,
- масса груза, 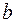 - коэффициент затухания.
- коэффициент затухания.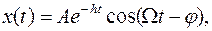
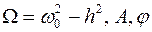 - произвольные постоянные.
- произвольные постоянные.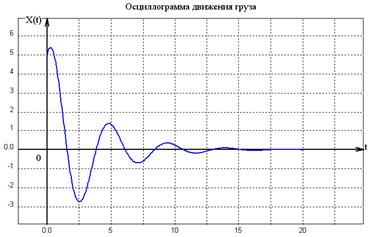
 . Поскольку на систему действует сила трения, то энергия системы убывает (расходуется на преодоление силы трения и превращается в тепло).
. Поскольку на систему действует сила трения, то энергия системы убывает (расходуется на преодоление силы трения и превращается в тепло).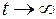 . Но практически можно считать, что колебания прекратились, если амплитуда их упала до достаточной доли начальной величины. Функция
. Но практически можно считать, что колебания прекратились, если амплитуда их упала до достаточной доли начальной величины. Функция 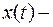 непериодическая, но она обладает свойством повторяемости: её максимумы, минимумы и нули наступают через равные промежутки времени, равные периоду множителя
непериодическая, но она обладает свойством повторяемости: её максимумы, минимумы и нули наступают через равные промежутки времени, равные периоду множителя 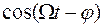 . Величину
. Величину 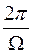 часто называют периодом затухающих колебаний. Из формулы
часто называют периодом затухающих колебаний. Из формулы 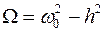 видно, что «период» затухающих колебаний больше периода незатухающих колебаний, равных
видно, что «период» затухающих колебаний больше периода незатухающих колебаний, равных 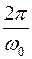 .
.


