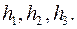Рассмотрим колебания грузика на пружине под действием внешней периодической с периодом  силы в предположении, что грузик не испытывает трения. Движение в этом случае описывается уравнением:
силы в предположении, что грузик не испытывает трения. Движение в этом случае описывается уравнением:
 (7)
(7)
Перепишем это уравнение в виде:
 (8)
(8)
где 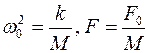 .
.
Известно, что общее решение уравнения (8) представляет собой сумму решений соответствующего однородного уравнения и частного решения неоднородного уравнения. Если  , то общее решение уравнения (8) запишем в виде:
, то общее решение уравнения (8) запишем в виде:
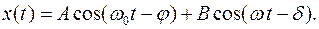 (9)
(9)
Из формулы (9) видно, что при  все решения уравнения (5) ограничены при
все решения уравнения (5) ограничены при 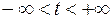 . Если частоты
. Если частоты  и
и  соизмеримы, то есть их отношение есть рациональное число, то
соизмеримы, то есть их отношение есть рациональное число, то  - периодическая функция. Действительно,
- периодическая функция. Действительно,  , где
, где 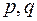 - целые числа, можно считать, что они положительны и взаимно просты. Тогда период колебаний равен:
- целые числа, можно считать, что они положительны и взаимно просты. Тогда период колебаний равен:  . Если частоты
. Если частоты  и
и  несоизмеримы, то есть их отношение есть иррациональное число, то
несоизмеримы, то есть их отношение есть иррациональное число, то  - непериодическая функция.
- непериодическая функция.
Допустим противное, и пусть  - период функции
- период функции  . Из тождества
. Из тождества  находим:
находим:
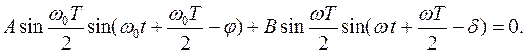 (10)
(10)
Выберем  так, чтобы
так, чтобы  , где
, где 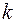 - целое число. Тогда первое слагаемое в (10) равно
- целое число. Тогда первое слагаемое в (10) равно  , и получаем соотношение
, и получаем соотношение
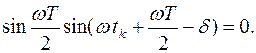 (11)
(11)
Если равен нулю первый сомножитель, то  , где
, где  - целое число. Это значение
- целое число. Это значение  - есть период второго слагаемого из (9), следовательно
- есть период второго слагаемого из (9), следовательно  - период первого слагаемого. Все периоды первого слагаемого из (9) имеют вид
- период первого слагаемого. Все периоды первого слагаемого из (9) имеют вид  , где
, где  - целое число. Поэтому
- целое число. Поэтому  при некотором целом
при некотором целом  , так что отношение
, так что отношение  - рациональное число. Это противоречит несоизмеримости частот
- рациональное число. Это противоречит несоизмеримости частот  и
и  .
.
Пусть второй сомножитель из (11) равен нулю. Тогда  , где
, где 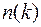 - целое число. Положим
- целое число. Положим 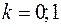 и вычитая первое тождество из второго, получаем
и вычитая первое тождество из второго, получаем  , где
, где  - целое число. Поэтому отношение
- целое число. Поэтому отношение  - рациональное число, а это противоречит предположению об их несоизмеримости. Значит,
- рациональное число, а это противоречит предположению об их несоизмеримости. Значит,  - непериодическая функция.
- непериодическая функция.
Вернемся к общему решению уравнения (8). Записав его в виде:
 (12)
(12)
Определим постоянные интегрирования, если 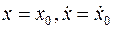 при
при  . Подставляя начальные условия в (12) и в выражение для скорости движения
. Подставляя начальные условия в (12) и в выражение для скорости движения  , получим
, получим 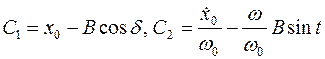 . Подставляя
. Подставляя  и
и  в соотношение (12), будем иметь
в соотношение (12), будем иметь
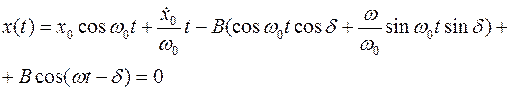 (13)
(13)
Такая запись решения позволяет установить, что даже при нулевых начальных условиях  грузик будет совершать колебания, происходящие с собственной частотой
грузик будет совершать колебания, происходящие с собственной частотой  . Эти колебания определяются членом
. Эти колебания определяются членом  и заметим, что амплитуда этих колебаний не зависит от начальных условий. При частоте
и заметим, что амплитуда этих колебаний не зависит от начальных условий. При частоте  , близкой к собственной частоте
, близкой к собственной частоте  , благодаря наложению колебаний наступает явление, называемой биением.
, благодаря наложению колебаний наступает явление, называемой биением.
Пусть  (но
(но  ), тогда выражение (13) при
), тогда выражение (13) при  и
и 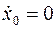 примет вид:
примет вид: 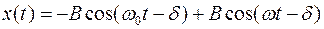 =
= 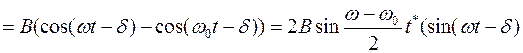 .
.
График этого движения представлен на рисунке 3:

Рис.3
Показанные на этом рисунке биения представляют собой колебания, происходящие с частотой  возмущающей силы, причем амплитуда этих колебаний медленно меняется по периодическому закону:
возмущающей силы, причем амплитуда этих колебаний медленно меняется по периодическому закону:  .
.
Подробнее исследуем второе слагаемое (9), описывающее чисто вынужденные колебания и не зависящие от начальных условий.
Амплитуда чисто вынужденных колебаний равна:
 (14)
(14)
График зависимости амплитуды вынужденных колебаний от  имеет вид:
имеет вид:

Рис.4
Из графика видно, что при  амплитуда резко возрастает.
амплитуда резко возрастает.
Рассмотрим теперь случай, когда собственная частота совпадает с частотой возмущающей силы, т.е.  . Частотное решение уравнения (8) в этом случае надо искать в виде:
. Частотное решение уравнения (8) в этом случае надо искать в виде:
 . (15)
. (15)
Подставляя (15) в уравнение (8) найдем, что
 .
.
Тогда частное решение уравнения (8) имеет вид:
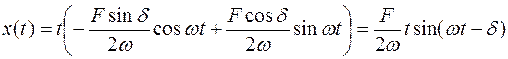 .
.
Общее решение уравнения (8) при  имеет вид:
имеет вид:
 .
.
График этого движения при  показан на рисунке 5.
показан на рисунке 5.
Как видно из рисунка 5, при  происходит неограниченное нарастание амплитуды колебаний по линейному закону во времени. Это явление носит название резонанса. происходит неограниченное нарастание амплитуды колебаний по линейному закону во времени. Это явление носит название резонанса.
|
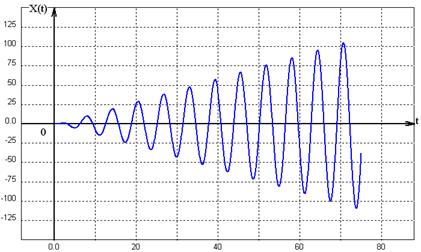
Рис.5
4. ДИССИПАТИВНЫЙ, ПЕРИОДИЧЕСКИ ВОЗМУЩАЕМЫЙ ЛИНЕЙНЫЙ ОСЦИЛЛЯТОР.
Рассмотрим колебания груза на пружине под действием внешней гармонической силы с учетом силы трения, описываемые линейным дифференциальным уравнением вида:
 , (16)
, (16)
где 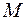 - масса груза,
- масса груза, 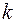 - коэффициент жесткости пружины,
- коэффициент жесткости пружины,  - амплитуда внешнего гармонического воздействия,
- амплитуда внешнего гармонического воздействия,  - его частота,
- его частота, 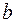 - коэффициент сопротивления.
- коэффициент сопротивления.
Уравнение (16) запишем в виде:
 , (17)
, (17)
где 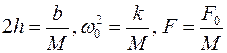 . К такому же уравнению придем для малых колебаний математического маятника, электрического контура и т.д.
. К такому же уравнению придем для малых колебаний математического маятника, электрического контура и т.д.
Предположим, что  . Ясно, что если трение очень велико, система вообще не осциллирует. Энергия пружинки едва хватает на борьбу с силами трения, и грузик будет медленно ползти к положению равновесия. Известно, что общее решение уравнения (17) можно записать в виде:
. Ясно, что если трение очень велико, система вообще не осциллирует. Энергия пружинки едва хватает на борьбу с силами трения, и грузик будет медленно ползти к положению равновесия. Известно, что общее решение уравнения (17) можно записать в виде:  , где первое слагаемое – общее решение соответствующего однородного однородного уравнения:
, где первое слагаемое – общее решение соответствующего однородного однородного уравнения:
 , (18)
, (18)
 - такие колебания совершает линейный автономный осциллятор (18) около устойчивого положения равновесия. Эти колебания называются собственными или свободными колебаниями осциллятора.
- такие колебания совершает линейный автономный осциллятор (18) около устойчивого положения равновесия. Эти колебания называются собственными или свободными колебаниями осциллятора.
Амплитуда 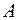 и сдвиг фазы
и сдвиг фазы 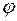 определяются из начальных условий:
определяются из начальных условий:
 .
.
При  и неограниченном возрастании
и неограниченном возрастании  собственные колебания затухают и все решения стремятся к вынужденному решению
собственные колебания затухают и все решения стремятся к вынужденному решению  , где
, где
 . (19)
. (19)
Рассмотрим три случая:
1) 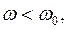 2)
2)  3)
3) 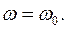
В первом случае внешняя сила идет главным образом на преодоление упругой силы. Во втором случае внешняя сила тратится в основном на придание грузику ускорения.
Из формулы (19) следует, что амплитуда установившихся колебаний в третьем случае больше, чем в первых двух. Когда частота  приближается к
приближается к  , то есть
, то есть  уменьшается, амплитуда колебаний возрастает и приходит максимум (рисунок 6). Вблизи значения
уменьшается, амплитуда колебаний возрастает и приходит максимум (рисунок 6). Вблизи значения 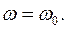 этот максимум наступает раньше
этот максимум наступает раньше  , так как выражение в знаменателе
, так как выражение в знаменателе

Рис.6
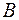 проходит через минимум
проходит через минимум  . Зависимость амплитуды вынужденных колебаний от соотношения
. Зависимость амплитуды вынужденных колебаний от соотношения  и
и  называется амплитудно-частотной характеристикой (АЧХ). Эта резонансная кривая оказывается характерной для резонансных эффектов, наблюдаемых при вынужденных колебаниях разнообразных колебательных систем.
называется амплитудно-частотной характеристикой (АЧХ). Эта резонансная кривая оказывается характерной для резонансных эффектов, наблюдаемых при вынужденных колебаниях разнообразных колебательных систем.
Возрастание амплитуды вынужденных колебаний в области, где  близки к близки к  , представляет наиболее типичную черту явления резонанса. , представляет наиболее типичную черту явления резонанса.
|
Явление резонанса можно рассматривать как случай, когда под действием гармонической силы система совершает почти собственные колебания. В области резонанса уравнение (16) члены  и
и  хотя и велики, но примерно равны по величине и противоположны по знаку. Они компенсируют друг друга, т.е. сама пружина, помимо внешней силы, сообщает грузу
хотя и велики, но примерно равны по величине и противоположны по знаку. Они компенсируют друг друга, т.е. сама пружина, помимо внешней силы, сообщает грузу 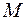 необходимое ускорение. Роль внешней силы сводится только к преодолению силы трения. При этом внешняя сила совершает наибольшую работу, т.к. направление движения груза все время совпадает с направлением внешней силы. Явление резонанса обусловлено тем, что при совпадении частот
необходимое ускорение. Роль внешней силы сводится только к преодолению силы трения. При этом внешняя сила совершает наибольшую работу, т.к. направление движения груза все время совпадает с направлением внешней силы. Явление резонанса обусловлено тем, что при совпадении частот  и
и  наступают наиболее благоприятные условия для поступления в систему энергии от источника внешней силы.
наступают наиболее благоприятные условия для поступления в систему энергии от источника внешней силы.
Посмотрим, как зависят резонансные колебания от величины затухания  . Амплитуда
. Амплитуда 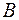 зависит не только от соотношения между
зависит не только от соотношения между  и
и  , но и от величины сил трения в системе. Как видно из (19) чем больше затухание
, но и от величины сил трения в системе. Как видно из (19) чем больше затухание  при прочих равных условиях, тем меньше амплитуда вынужденных колебаний. На рисунке 7 изображены осциллограммы движения
при прочих равных условиях, тем меньше амплитуда вынужденных колебаний. На рисунке 7 изображены осциллограммы движения  при трех значениях
при трех значениях  .
.
С увеличением сил трения резонансные кривые опускаются вниз, но максимум этой кривой опускается гораздо резче, чем области далекие от резонанса. Кривая резонанса при увеличении сил трения притупляется. С увеличением затухания системы все явления резонанса становятся менее заметными и при больших затуханиях вообще исчезают.
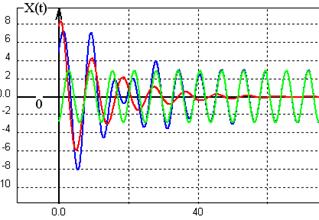
Рис.7a


Рис.7б Рис.7в
На рисунке 8 изображены резонансные кривые при значениях  , равных
, равных 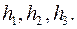

Рис.8
| Резонансными свойствами, т.е. способностью особенно сильно отзываться на колебания одной определенной частоты, обладают только системы с малым затуханием.
|
Поэтому для использования резонанса, например для измерения частоты колебаний, необходимо применять резонаторы (колебательные системы, частота которых заранее известна) с возможно меньшим затуханием. Наоборот, в тех случаях, когда явление резонанса играет вредную роль и его надо устранить, следует увеличить затухание колебательной системы.

 силы в предположении, что грузик не испытывает трения. Движение в этом случае описывается уравнением:
силы в предположении, что грузик не испытывает трения. Движение в этом случае описывается уравнением: (7)
(7) (8)
(8)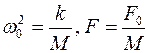 .
. , то общее решение уравнения (8) запишем в виде:
, то общее решение уравнения (8) запишем в виде: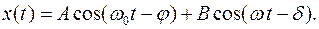 (9)
(9)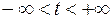 . Если частоты
. Если частоты  и
и  соизмеримы, то есть их отношение есть рациональное число, то
соизмеримы, то есть их отношение есть рациональное число, то  - периодическая функция. Действительно,
- периодическая функция. Действительно,  , где
, где 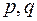 - целые числа, можно считать, что они положительны и взаимно просты. Тогда период колебаний равен:
- целые числа, можно считать, что они положительны и взаимно просты. Тогда период колебаний равен:  . Если частоты
. Если частоты  - период функции
- период функции  находим:
находим: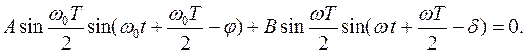 (10)
(10) так, чтобы
так, чтобы  , где
, где 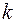 - целое число. Тогда первое слагаемое в (10) равно
- целое число. Тогда первое слагаемое в (10) равно  , и получаем соотношение
, и получаем соотношение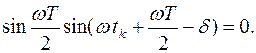 (11)
(11) , где
, где  - целое число. Это значение
- целое число. Это значение  - есть период второго слагаемого из (9), следовательно
- есть период второго слагаемого из (9), следовательно  , где
, где  - целое число. Поэтому
- целое число. Поэтому  при некотором целом
при некотором целом  , так что отношение
, так что отношение  - рациональное число. Это противоречит несоизмеримости частот
- рациональное число. Это противоречит несоизмеримости частот  , где
, где 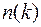 - целое число. Положим
- целое число. Положим 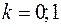 и вычитая первое тождество из второго, получаем
и вычитая первое тождество из второго, получаем  , где
, где  (12)
(12)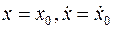 при
при  . Подставляя начальные условия в (12) и в выражение для скорости движения
. Подставляя начальные условия в (12) и в выражение для скорости движения  , получим
, получим 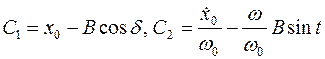 . Подставляя
. Подставляя  и
и  в соотношение (12), будем иметь
в соотношение (12), будем иметь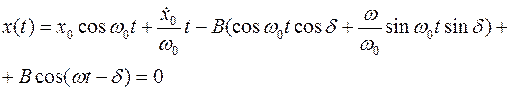 (13)
(13) грузик будет совершать колебания, происходящие с собственной частотой
грузик будет совершать колебания, происходящие с собственной частотой  . Эти колебания определяются членом
. Эти колебания определяются членом  и заметим, что амплитуда этих колебаний не зависит от начальных условий. При частоте
и заметим, что амплитуда этих колебаний не зависит от начальных условий. При частоте  (но
(но  ), тогда выражение (13) при
), тогда выражение (13) при  и
и 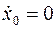 примет вид:
примет вид: 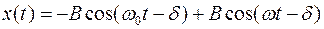 =
= 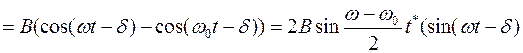 .
.
 .
. (14)
(14)
 амплитуда резко возрастает.
амплитуда резко возрастает. . Частотное решение уравнения (8) в этом случае надо искать в виде:
. Частотное решение уравнения (8) в этом случае надо искать в виде: . (15)
. (15) .
.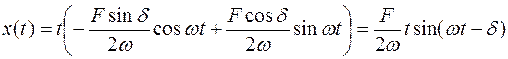 .
. .
. показан на рисунке 5.
показан на рисунке 5.
 , (16)
, (16)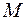 - масса груза,
- масса груза,  - амплитуда внешнего гармонического воздействия,
- амплитуда внешнего гармонического воздействия, 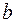 - коэффициент сопротивления.
- коэффициент сопротивления. , (17)
, (17)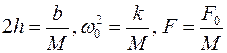 . К такому же уравнению придем для малых колебаний математического маятника, электрического контура и т.д.
. К такому же уравнению придем для малых колебаний математического маятника, электрического контура и т.д. . Ясно, что если трение очень велико, система вообще не осциллирует. Энергия пружинки едва хватает на борьбу с силами трения, и грузик будет медленно ползти к положению равновесия. Известно, что общее решение уравнения (17) можно записать в виде:
. Ясно, что если трение очень велико, система вообще не осциллирует. Энергия пружинки едва хватает на борьбу с силами трения, и грузик будет медленно ползти к положению равновесия. Известно, что общее решение уравнения (17) можно записать в виде:  , где первое слагаемое – общее решение соответствующего однородного однородного уравнения:
, где первое слагаемое – общее решение соответствующего однородного однородного уравнения: , (18)
, (18) - такие колебания совершает линейный автономный осциллятор (18) около устойчивого положения равновесия. Эти колебания называются собственными или свободными колебаниями осциллятора.
- такие колебания совершает линейный автономный осциллятор (18) около устойчивого положения равновесия. Эти колебания называются собственными или свободными колебаниями осциллятора.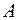 и сдвиг фазы
и сдвиг фазы 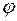 определяются из начальных условий:
определяются из начальных условий: .
. и неограниченном возрастании
и неограниченном возрастании  собственные колебания затухают и все решения стремятся к вынужденному решению
собственные колебания затухают и все решения стремятся к вынужденному решению  , где
, где . (19)
. (19)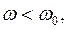 2)
2)  3)
3) 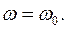
 уменьшается, амплитуда колебаний возрастает и приходит максимум (рисунок 6). Вблизи значения
уменьшается, амплитуда колебаний возрастает и приходит максимум (рисунок 6). Вблизи значения 
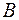 проходит через минимум
проходит через минимум  . Зависимость амплитуды вынужденных колебаний от соотношения
. Зависимость амплитуды вынужденных колебаний от соотношения  и
и  хотя и велики, но примерно равны по величине и противоположны по знаку. Они компенсируют друг друга, т.е. сама пружина, помимо внешней силы, сообщает грузу
хотя и велики, но примерно равны по величине и противоположны по знаку. Они компенсируют друг друга, т.е. сама пружина, помимо внешней силы, сообщает грузу  и
и  . Амплитуда
. Амплитуда  .
.