Дисперсия света. Изучить явление дисперсии света и эффект спектрального разложения параллельного пучка света стеклянной призмой
Лабораторная работа № 1 ИЗУЧЕНИЕ ДИСПЕРСИИ СВЕТА И ОПРЕДЕЛЕНИЕ ДЛИНЫ ВОЛНЫ С ПОМОЩЬЮ СПЕКТРОСКОПА Цель работы Изучить явление дисперсии света и эффект спектрального разложения параллельного пучка света стеклянной призмой. Измерить угол наименьшего отклонения лучей призмой для различных длин световых волн и определить по результатам этих измерений показатель преломления. ОБОРУДОВАНИЕ И ПРИНАДЛЕЖНОСТИ Спектроскоп, ртутная лампа, источник света с неизвестным спектром (лампа дневного света или неоновая лампа). ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Дисперсия света Электромагнитная световая волна, падая из вакуума на вещество, вызывает колебания его атомов и молекул. Атомы и молекулы, приходя в вынужденные колебания, становятся вторичными излучателями электромагнитных волн. Электромагнитная волна, возникающая в результате суперпозиции первичной и вторичной волн и распространяющаяся в той среде, откуда пришла первичная волна, называется отражённой волной. Электромагнитная волна, возникшая в результате суперпозиции первичной и вторичной волн и распространяющаяся в той среде, откуда пришла вторичная волна, называется преломлённой волной. Колебания частиц вещества под действием электромагнитной волны возбуждаются в основном электрической компонентой электромагнитного поля волны. Электрические свойства вещества, определяющие его поведение под действием световой волны, характеризуются диэлектрической проницаемостью среды.e Для всех веществ в области оптических частот электромагнитных волн магнитная проницаемость среды
где
называется абсолютным показателем преломления света для данной среды. Отношение
где Дисперсией света называется зависимость показателя преломления n вещества от частоты v (или длины волны l) света, т.е.
Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму. Опытное изучение явления дисперсии света впервые осуществил Ньютон в 1666 г., пропуская «белый» (солнечный) свет через призму. Пучок лучей от линейного источника S направлялся на призму P и после отклонения падал на экран Э (рис. 1.1). На экране при этом наблюдался спектр, т.е. широкая полоса, окрашенная в цвета радуги, от красного до фиолетового цвета. Если сравнить между собой спектры, получаемые от призм, изготовленных из разных оптически прозрачных материалов, то оказывается, что не только лучи одной и той же частоты отклоняются этими призмами на различный угол, но и ширина участков спектров, соответствующих одинаковому интервалу частот
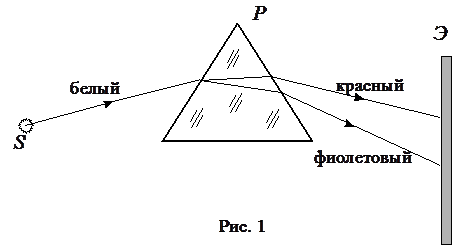 Спектр, наблюдавшийся Ньютоном, представлял собой сплошную радужную полосу. Такой спектр называется сплошным спектром. Сплошной спектр, например, имеет солнечное излучение. Спектр, наблюдавшийся Ньютоном, представлял собой сплошную радужную полосу. Такой спектр называется сплошным спектром. Сплошной спектр, например, имеет солнечное излучение.
Все химические элементы, находясь в газообразном состоянии, дают спектры не сплошные, а состоящие из ряда дискретных линий. Такие спектры получили название линейчатых, и для разных веществ они отличаются как числом линий, так и частотами. Это обстоятельство дало возможность разработать очень точный и чувствительный метод определения химического состава различных веществ, называемый спектральным анализом. Рассмотрим дисперсию света в призме. Пусть монохроматический пучок света падает на призму с преломляющим углом g и показателем преломления n (рис. 1.2) под углом a1. После двукратного преломления (на левой и правой гранях призмы) луч оказывается отклоненным от первоначального направления на угол j. В соответствии с законом преломления света:
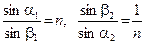 . (1.5) . (1.5)
Рассмотрим рисунок. Из четырехугольника ACFD, у которого углы C и D – прямые, имеем: g + F = p; а из треугольника CDF –
Предположим, что углы g и a 1 малы, тогда углы a2, b1 и b2 будут также малы и вместо синусов этих углов в (1.5) можно воспользоваться их значениями. Поэтому a1/b1=n, b2/a2=1 /n, а так как b1+b2=g, то a2=b2 n=n (g-b1)= n (g-a1/ n) =n g-a1, откуда
|

 . Скорость распространения света в среде
. Скорость распространения света в среде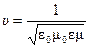 , (1.1)
, (1.1)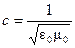 - скорость распространения света в вакууме, а
- скорость распространения света в вакууме, а 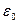 и
и 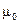 соответственно электрическая и магнитная постоянные. Отношение
соответственно электрическая и магнитная постоянные. Отношение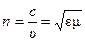 (1.2)
(1.2)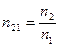 , (1.3)
, (1.3)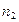 и
и 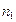 - абсолютные показатели преломления сред, в которых распространяется свет, называется относительным показателем преломления второй среды по отношению к первой. Относительный показатель преломления (n 21) больше единицы для всех сред, кроме вакуума, где n 21 = 1. Чем больше значение n для среды, тем более оптически плотной она является. Относительная диэлектрическая проницаемость e, а с нею и
- абсолютные показатели преломления сред, в которых распространяется свет, называется относительным показателем преломления второй среды по отношению к первой. Относительный показатель преломления (n 21) больше единицы для всех сред, кроме вакуума, где n 21 = 1. Чем больше значение n для среды, тем более оптически плотной она является. Относительная диэлектрическая проницаемость e, а с нею и 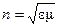 , оказываются зависимыми от частоты падающего света.
, оказываются зависимыми от частоты падающего света.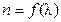 . (1.4)
. (1.4) , будет различной. Это означает, что разные материалы обладают различной дисперсией.
, будет различной. Это означает, что разные материалы обладают различной дисперсией.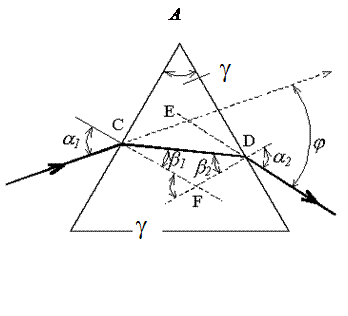
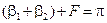 , поэтому
, поэтому 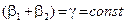 , где g – преломляющий угол призмы, тогда
, где g – преломляющий угол призмы, тогда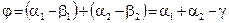 . (1.6)
. (1.6)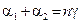 . (1.7)
. (1.7)


