Решение уравнения (1.15) можно записать в виде
где
в чем легко убедиться подстановкой. Подставляя (1.16) и (1.17) в (1.14), получим
Если в веществе имеются различные заряды ei, совершающие вынужденные колебания с различными собственными частотами w0 i , то
где mi – масса i‑го заряда.
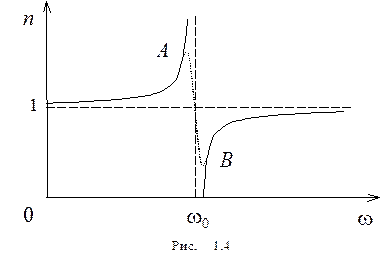 Из выражений (1.18) и (1.19) вытекает, что показатель преломления n зависит от частоты w внешнего поля, т.е. полученные зависимости действительно подтверждают явление дисперсии света, хотя и при указанных выше допущениях, которые в дальнейшем надо устранить. Из выражений (1.18) и (1.19) следует, что в области от w = 0 до w = w0 n2 больше единицы и возрастает с увеличением w (нормальная дисперсия); при w = w0 n 2 = ± ¥; в области от w = w0 до w = ¥ n 2 меньше единицы и возрастает от ‑ ¥ до 1 (нормальная дисперсия). Перейдя от n 2 к n, получим, что график зависимости n от w имеет вид, изображенный на рис. 1.4. Такое поведение n вблизи w0 – результат допущения об отсутствии сил сопротивления при колебаниях электронов. Если принять в расчет и это обстоятельство, то график функции n (w) вблизи w0 задается штриховой линией AB. Область AB – область аномальной дисперсии (n убывает при возрастании w), остальные участки зависимости n от w описывают нормальную дисперсию (n возрастает с возрастанием w). Из выражений (1.18) и (1.19) вытекает, что показатель преломления n зависит от частоты w внешнего поля, т.е. полученные зависимости действительно подтверждают явление дисперсии света, хотя и при указанных выше допущениях, которые в дальнейшем надо устранить. Из выражений (1.18) и (1.19) следует, что в области от w = 0 до w = w0 n2 больше единицы и возрастает с увеличением w (нормальная дисперсия); при w = w0 n 2 = ± ¥; в области от w = w0 до w = ¥ n 2 меньше единицы и возрастает от ‑ ¥ до 1 (нормальная дисперсия). Перейдя от n 2 к n, получим, что график зависимости n от w имеет вид, изображенный на рис. 1.4. Такое поведение n вблизи w0 – результат допущения об отсутствии сил сопротивления при колебаниях электронов. Если принять в расчет и это обстоятельство, то график функции n (w) вблизи w0 задается штриховой линией AB. Область AB – область аномальной дисперсии (n убывает при возрастании w), остальные участки зависимости n от w описывают нормальную дисперсию (n возрастает с возрастанием w).
|

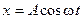 , (1.16)
, (1.16) , (1.17)
, (1.17) . (1.18)
. (1.18)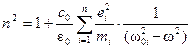 , (1.19)
, (1.19)


