Свойства определителей. Для определителей справедливы следующие утверждения, называемые свойствами определителей.

Для определителей справедливы следующие утверждения, называемые свойствами определителей.

1. Определитель не изменяется при транспонировании: detA^T=detA.

2. Если строка (столбец) матрицы A равна линейной комбинации соответственных строк (столбцов) матриц A и B, а остальные строки (столбцы) этих матриц совпадают, то ее определитель равен линейной комбинации определителей матриц A и B:

A_i = a·B_i + b·C_i, detA = a·detB + b·detC,

A^(j) = a·B^(j) + b·C^(j), detA = a·detB + b·detC.

3. При перестанровке любых двух строк (столбцов), определитель меняет знак.

4. Если в определителе есть две одинаковые строки (два одинаковых столбца), то он равен нулю.

5. Если в определителе есть две пропорциональные строки (два пропорциональные столбца), то он равен нулю.

6. Определитель не изменится, если к элементам любой его строки (столбца) прибавить элементы любой другой строки (столбца), умноженные на одно и то же число.

7. Определитель, содержащий нулевую строку (нулевой столбец), равен нулю.

8. Сумма произведений элементов любой строки (столбца) на алгебраические дополнения другой строки (другого столбца) равна нулю.

9. Определитель произведения матриц равен произведению определителей сомножителей.

Перечисленные свойства позволяют упростить вычисление определителя.

Пример. 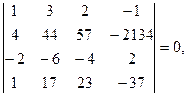поскольку 1-я и 3-я строки пропорциональны.