Системы линейных уравнений, методы их решения.
Основные понятия Рассмотрим систему m линейных уравнений с n неизвестными:
xj – неизвестное системы; aij – коэффициент при неизвестном;
Рассмотрим различные формы записи системы (1):
а) Краткая запись
б) Матричная форма записи Составим матрицу из коэффициентов при неизвестных:
– основная матрица системы (1). Составим матрицу-столбец неизвестных системы
и матрицу-столбец свободных членов
Тогда матричная форма записи системы (1) имеет вид: А ∙ Х = В
в) Векторная форма записи (1``) Рассмотрим следующие векторы-столбцы системы (1) вида:
Х = (x1, x2, x3, …, xn) – n переменных. Составим линейную комбинацию векторов условий вида: А1 ∙ х 1 + А2 ∙ х 2 + … + А n ∙ хn где х 1, х 2, …, хn коэффициенты системы (1).
Линейная комбинация векторов – новый вектор, т.е. система (1) в векторной форме имеет вид: А1 ∙ х 1 + А2 ∙ х 2 + … + А n ∙ хn = Решить систему линейных уравнений значит найти ее решения, или убедиться, что их нет. Решением системы линейных уравнений (СЛУ) называется такой вектор Х1 – α1, Х2 – α2, …, Х n – α n. Система уравнений называется совместной, если существует хотя бы одно решение (одно или ∞). СЛУ называется несовместной, если она не имеет ни одного решения. Совокупная система уравнений может иметь одно решение (совместная и определенная) или бесконечное множество решений (совместная и неопределенная). Случай, когда решений конечное множество невозможен. Две системы называются равносильными, если они имеют одни и те же решения.
|

 (1)
(1) j = 1, n;
j = 1, n; i = 1,m;
i = 1,m; bi – свободный член;
bi – свободный член;  i = 1, m.
i = 1, m. (1`)
(1`)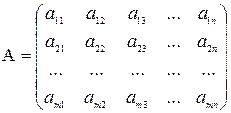
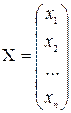

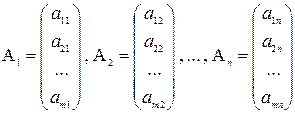
 (1```)
(1```) (α1; α2; …; α n), координаты которого обращают в тождество каждое уравнение системы, если в каждое уравнение системы подставить вместо
(α1; α2; …; α n), координаты которого обращают в тождество каждое уравнение системы, если в каждое уравнение системы подставить вместо


