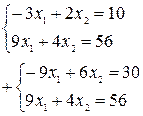Геометрический метод решения системы линейных неравенств с двумя переменными
Совокупность линейных неравенств с общими неизвестными называется системой линейных неравенств.
Неравенства могут быть одного смысла (≤ или ≥) или разного. Множество решений, которое удовлетворяет каждому неравенству системы, называется решением системы неравенств. Системы неравенств, имеющие хотя бы одно решение, называются совместными. Если системы неравенств не имеют решений, то они – несовместные. Если система m неравенств с двумя переменными совместна, то множеством решений такой системы является выпуклый многоугольник или выпуклая многоугольная область (неограниченная). Множеством решений системы линейных неравенств с двумя переменными может быть: 1) Точка; 2) Пустое множество; 3) Выпуклый многоугольник; 4) Выпуклая неограниченная область. Пример: Построить область решений системы линейных неравенств:
1)
x 1 = 0; x 2 = 5 x 2 = 0; x 1 = -10/5 О(0;0) ≤ 10 – верно 2)
x 1 = 0; x 2 = 6,2 x 2 = 0; x 1 = 14 О(0;0) ≤ 56 – верно 3)
x 1 = 0; x 2 = 4/3
О(0;0) ≥ 4 – неверно
Точки пересечения:
10 х 2 = 86 х 2 = 8,6 -3 х 1 = 7,2 х 1 = 2,4 (2,4; 8,6)
|

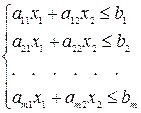


 – прямая l 1
– прямая l 1
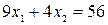 – прямая l 2
– прямая l 2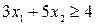
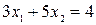 – прямая l 3
– прямая l 3 x 2 = 0; x 1 = 0,8
x 2 = 0; x 1 = 0,8