Скалярное произведение.
Скалярное (т.е. числовое) произведение
где |
В частности, длина вектора связана со скалярным произведением:
Механическое истолкование скалярного произведения: (Например, источники силы трения производят отрицательную работу и, значит, приобретают энергию - нагреваются; в этом примере cos j < 0.) Свойства скалярного произведения: 1) = k Свойства 2) и 3) получаются из формулы (4) и соответствующих свойств проекций. Они означают, что при скалярном умножении векторов скобки раскрываются, как при умножении чисел. Например, (2 Из определения (3) легко вывести «таблицу» скалярного умножения ортов
Разлагая векторы Правило. Имеет место алгебраическая формула для скалярного произведения векторов
Примененияскалярного произведения в геометрии. 1) Длина вектора ï (это - следствие формул (5) и (6)). 2)Расстояние между двумя точками A1 иA2: ï 3)Косинус угла между двумя векторами cos j = 4)Если два (ненулевых) вектора
Замечание. В задачах, в которых фигурируют только точки и векторы на координатной плоскости O xy, координата z (равная нулю) не пишется. В этой ситуации применяют формулы, аналогичные (6)-(9). Например, расстояние между двумя точками теперь вычисляется по формуле | A1A2 |= ï
|


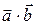 двух геометрических векторов
двух геометрических векторов и
и  определяетсякакпроизведение длин этих векторов и косинуса угла между ними:
определяетсякакпроизведение длин этих векторов и косинуса угла между ними:
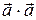 = |
= | 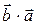 ; 2)
; 2) 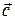 ) =
) = 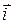 ,
,  ,
, 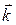 :
: ï =((x 2- x 1)2+(y 2- y 1)2+(z 2- z 1)2)1/2. (8)
ï =((x 2- x 1)2+(y 2- y 1)2+(z 2- z 1)2)1/2. (8)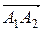 ï =((x 2 - x 1)2 + (y 2- y 1)2) 1/ 2. (10)
ï =((x 2 - x 1)2 + (y 2- y 1)2) 1/ 2. (10)


