Векторное произведение  ´
´  двух геометрических векторов
двух геометрических векторов  и
и  определяется как вектор с тремя характеристическими свойствами:
определяется как вектор с тремя характеристическими свойствами:
1) ê  ´
´  ê =ê
ê =ê  ê× ê
ê× ê  ê ×sin j - это площадь параллелограмма, построенного на векторах
ê ×sin j - это площадь параллелограмма, построенного на векторах  и
и  (j - угол между векторами
(j - угол между векторами  и
и  ); 2) вектор
); 2) вектор  ´
´  ортогонален к векторам
ортогонален к векторам  и
и  (и, следовательно, к плоскости, содержащей векторы
(и, следовательно, к плоскости, содержащей векторы  и
и  ; 3) кратчайший поворот от
; 3) кратчайший поворот от  к
к  выглядит со стороны вектора
выглядит со стороны вектора  ´
´  происходящим против часовой стрелки.
происходящим против часовой стрелки.
Связь векторного произведения со скалярным: |  ´
´  |2 + (
|2 + ( ×
×  )2 = |
)2 = |  |2 × |
|2 × |  |2.
|2.
Пример векторного произведения в механике. Пусть к твердому телу, закрепленному шарнирно в начале координат O, приложена сила.  - вектор силы,
- вектор силы,
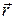 - вектор из Oв точку приложения силы; вращающий момент силы относительно точки Oесть вектор
- вектор из Oв точку приложения силы; вращающий момент силы относительно точки Oесть вектор  =
= 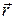 ´
´  , направленный вдоль оси вращения. Его абсолютная величина ê
, направленный вдоль оси вращения. Его абсолютная величина ê  ê равна произведению (величины) силы на «плечо».
ê равна произведению (величины) силы на «плечо».
Для векторного произведения можно написать формулу, аналогичную (4).
 ´
´ 
 = ê
= ê  ê×
ê× 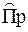 ^
^ 
 ; (11)
; (11) 
здесь вектор 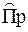 ^
^ 
 получается проектированием вектора
получается проектированием вектора  на плоскость, перпендикулярную к вектору
на плоскость, перпендикулярную к вектору  ,и последующим поворотом этой проекции в указанной плоскости на 90° против часовой стрелки (если смотреть со стороны вектора
,и последующим поворотом этой проекции в указанной плоскости на 90° против часовой стрелки (если смотреть со стороны вектора  ).
).
Если два вектора  и
и  коллинеарны, то
коллинеарны, то  ´
´  = 0. другие свойства таковы.
= 0. другие свойства таковы.
Свойства векторного произведения. 1)  ´
´  = -
= -  ´
´  ; 2)
; 2)  ´ k
´ k  = k
= k  ´
´  (k - число); 3)
(k - число); 3)  ´ (
´ ( +
+ 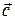 ) =
) =  ´
´  +
+  ´
´ 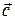 .
.
Свойства 2) и 3) получаются из формулы (11) и соответствующих свойств векторных проекций. Они означают, что при векторном умножении скобки раскрываются, как при умножении чисел. Например,(2  – 3
– 3  ) ´
) ´ 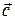 = 2
= 2  ´
´ 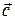 – 3
– 3  ´
´ 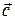 . (Однако сочетательного свойства для
. (Однако сочетательного свойства для  ´(
´( ´
´ 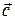 )нет.)
)нет.)
Из формулы (11) и определения легко вывести «таблицу» векторного умножения ортов 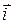 ,
,  ,
, 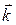 правой прямоугольной системы координат (далее рассматриваются правые системы):
правой прямоугольной системы координат (далее рассматриваются правые системы): 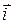 ´
´ 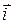 =
=  ´
´  =
= 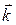 ´
´ 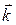 = 0;
= 0;
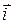 ´
´  =
= 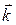 ,
,  ´
´ 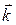 =
= 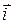 ,
, 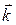 ´
´ 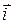 =
=  ;
;  ´
´ 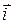 =-
=- 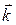 ,
, 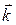 ´
´  =-
=- 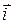 ,
, 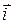 ´
´ 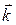 =-
=-  .
.
Разлагая векторы  и
и  по ортам и используя «таблицу» векторного умножения ортов, получаем выражение для
по ортам и используя «таблицу» векторного умножения ортов, получаем выражение для  ´
´  , которое компактно записывается с помощью определителя (после раскрытия его получится вектор).
, которое компактно записывается с помощью определителя (после раскрытия его получится вектор).
Правило. Имеет место алгебраическая формула для векторного произведения векторов  (x 1; y 1; z 1)и
(x 1; y 1; z 1)и  (x 2; y 2; z 2):
(x 2; y 2; z 2):
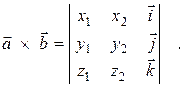 (12)
(12)
Применения векторного произведения в геометрии.
1) Площадь параллелограмма, построенного на векторах  и
и  :
:
S = |  ´
´  |. (13)
|. (13)
2) Площадь треугольника A1A2A3: S = 1/ 2 ×|  |.
|.
3) Вектор  , перпендикулярный к плоскости треугольника A1A2A3:
, перпендикулярный к плоскости треугольника A1A2A3:  .
.

 ´
´  двух геометрических векторов
двух геометрических векторов  - вектор силы,
- вектор силы,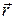 - вектор из Oв точку приложения силы; вращающий момент силы относительно точки Oесть вектор
- вектор из Oв точку приложения силы; вращающий момент силы относительно точки Oесть вектор  =
= 
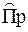 ^
^ 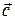 ) =
) = 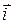 ,
,  ,
, 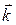 правой прямоугольной системы координат (далее рассматриваются правые системы):
правой прямоугольной системы координат (далее рассматриваются правые системы): 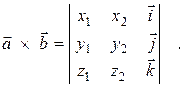 (12)
(12) |.
|. , перпендикулярный к плоскости треугольника A1A2A3:
, перпендикулярный к плоскости треугольника A1A2A3:  .
.


