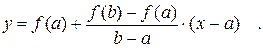Уравнение прямой на плоскости.
Предположим,чтоизвестна одна точка M0(x 0; y 0 ) на некоторой прямой L на координатной плоскости O xy, и известен ненулевой вектор A ×(x - x 0) + B ×(y - y 0 ) = 0. (3) Отсюда следует так называемое общее уравнение прямой на плоскости: A x + B y + C = 0. (4) Это уравнение линейное (т.е. 1-й степени), поэтому прямую называют линией 1-го порядка. Числа A, B – коэффициенты уравнения, причем хотя бы одно из них не равно нулю, а число C обозначает постоянную величину - A x 0 - B y 0 в (3). Для точек M(x; y), не лежащих на прямой, расстояние d до прямой равно d = | A x + B y + C | / · Пояснение. Пусть M0 - произвольная точка плоскости, тогда d= |Пр =| (а) Вертикальные прямые. Если в уравнении (4) B = 0, то уравнение принимает вид x = x 0 , где x 0= - C / A есть постоянная величина. (б) Невертикальные прямые. Если в уравнении (4) B ¹ 0,то уравнение прямой приводится к т. наз. уравнению с угловым коэффициентом y = k x + b (6) (k = - A / B, b = - C / B).Числа k и b определяют прямую, поэтому их называют параметрами прямой. Рассматриваемая прямая – график линейной функции. Чтобы изобразить ее, нужно на координатной плоскости отметить две точки, например, (0; b) при x =0 и (1; b + k) при x =1, и соединить их с помощью линейки. Отсюда следует геометрический смысл k: k есть тангенс угла наклона j прямой L(т.е. угла между прямой Lи полуосью O x + ): k = tg j (7) (- 90° < j < 90°, - ¥ < tg j < + ¥). Множитель k называется угловым коэффициентом прямой. Свойства углового коэффициента. 1) Если две прямые параллельны, то их угловые коэффициенты равны: k 1 = k 2. 2) Если две прямые перпендикулярны, то их угловые коэффициенты связаны соотношением k 2 = - 1 / k 1. 3) Угол a между двумя прямыми на плоскости находится по формуле tg a = (k 1 - k 2) / (1 + k 1 k 2 ). Рассмотрим три способа составления уравнения прямой в зависимости от исходных данных. 1-я ситуация. Известны одна точка M0(x 0 ; y 0) на прямой и угловой коэффициент k прямой L.Тогда уравнение прямой пишется так: y – y 0= k × (x – x 0). · Пояснение. В формуле (6) параметр k известен, а параметр b не известен. Чтобы исключить его из (6), учтем, что точка M0 лежит на прямой: y 0= k x 0+ b. Вычтем это уравнение из (6). Получим: y - y 0= k ×(x - x 0). · 2-я ситуация. Известны одна точка M0 (x 0 ; y 0 ) на прямой L и ненулевой вектор
· Пояснение. Для точек M (x; y) на прямой L вектор y - y 0 = t × m. (это – т.наз. параметрические уравнения прямой на плоскости.)Исключая отсюда t, получим (8). Может оказаться, что один из знаменателей в (8) равен нулю, например, l = 0. Запись (x – x 0)/ 0 =(y - y 0) / m есть условность(ее нельзя понимать буквально). Чтобы «расшифровать» ее, возвращаемся к параметрическим уравнениям прямой и получаем корректное уравнение данной прямой: x - x 0 = 0.· 3-я ситуация. Известны две точки M0(x 0 ; y 0) и M1(x 1 ; y 1 ) на прямой L. Тогда уравнение прямой также пишется в каноническом виде, причем роль направляющего вектора
В частности, если известны две точки M0 (a; 0) и M1(0; b) прямой, принадлежащие координатным осям O x иO y, соответственно, то пишут так называемое уравнение прямой в отрезках: x a + y b = 1.
3.Применение: линейное интерполирование функций. Пусть известно, что график некоторой функции y = f (x) на отрезке [ a; b ] незначительно отличается от отрезка прямой. Заменим график функции на отрезке отрезком прямой, соединяющей точки M0(a; f (a)) и M1(b; f (b)). Согласно (9), уравнение этой прямой есть Эту формулу называют линейной интерполяцией (или линейным приближением) данной функции на данном отрезке. На практике используют таблицу значений линейной интерполяции. Для этого отрезок [ a; b ] разбивают на некоторое число n равныхотрезков. Длина каждого отрезка (b - a) / n обозначается как D x (знак D означает «изменение»). Когда x изменяется на величину D x, данная функция в линейном приближении изменяется на величину
Таблица линейной интерполяции функции принимает следующий вид.
|

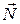 (A; B), перпендикулярный к прямой (он называется нормальным вектором прямой). Для любой точки M(x; y) прямой Lвекторы
(A; B), перпендикулярный к прямой (он называется нормальным вектором прямой). Для любой точки M(x; y) прямой Lвекторы 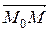 перпендикулярны, и их скалярное произведение
перпендикулярны, и их скалярное произведение  (5)
(5)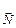
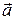 (l; m),параллельный прямой (такой вектор называется направляющим). В этой ситуации пишут так называемое каноническое уравнение прямой на плоскости:
(l; m),параллельный прямой (такой вектор называется направляющим). В этой ситуации пишут так называемое каноническое уравнение прямой на плоскости: (8)
(8)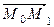 (x 1– x 0 ; y 1 - y 0):
(x 1– x 0 ; y 1 - y 0):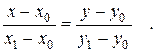 (9)
(9)