1-я ситуация. Известны точка M0(x 0; y 0; z 0) на прямой L в пространстве и ненулевой вектор 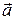 (l; m; n), параллельныйпрямой (он называется направляющим вектором прямой).Тогда координаты точек прямой удовлетворяют уравнениям, называемым каноническими уравнениями прямой в пространстве:
(l; m; n), параллельныйпрямой (он называется направляющим вектором прямой).Тогда координаты точек прямой удовлетворяют уравнениям, называемым каноническими уравнениями прямой в пространстве:
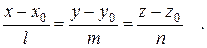 (14)
(14)
· Пояснение. Эта ситуация аналогична 2-й ситуации в п. 3.2. Для точек M(x; y; z)
прямой L вектор 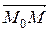 коллинеарен вектору
коллинеарен вектору 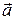 и потому пропорционален ему:
и потому пропорционален ему:
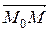 = t ×
= t × 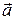 . Записывая это через координаты векторов, получаем параметрические уравнения прямой в пространстве: x - x 0 = t × l, y - y 0= t × m, z - z 0 = t × n. Исключая отсюда параметр t, получаем (14). Это – система двух линейных уравнений с тремя переменными. Может оказаться, что один из знаменателей в (14) равен нулю, например, l = 0. Тогда запись (x - x 0) / 0=(y - y 0) / m =(z - z 0) / n является условной (ее
. Записывая это через координаты векторов, получаем параметрические уравнения прямой в пространстве: x - x 0 = t × l, y - y 0= t × m, z - z 0 = t × n. Исключая отсюда параметр t, получаем (14). Это – система двух линейных уравнений с тремя переменными. Может оказаться, что один из знаменателей в (14) равен нулю, например, l = 0. Тогда запись (x - x 0) / 0=(y - y 0) / m =(z - z 0) / n является условной (ее
нельзя понимать буквально). В этом случае, привлекая снова параметрические
уравнения прямой, эту запись можно «расшифровать» так:
x - x 0=0, (y - y 0) / m = (z - z 0) / n. Может оказаться, что два знаменателя в (16) равны нулю, например, l = m = 0; тогда условная запись (x - x 0) / 0 = (y - y 0) / 0 = (z - z 0) / n системы «расшифровывается» так: x - x 0=0, y - y 0=0. ·

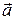 (l; m; n), параллельныйпрямой (он называется направляющим вектором прямой).Тогда координаты точек прямой удовлетворяют уравнениям, называемым каноническими уравнениями прямой в пространстве:
(l; m; n), параллельныйпрямой (он называется направляющим вектором прямой).Тогда координаты точек прямой удовлетворяют уравнениям, называемым каноническими уравнениями прямой в пространстве: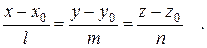 (14)
(14)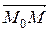 коллинеарен вектору
коллинеарен вектору 


