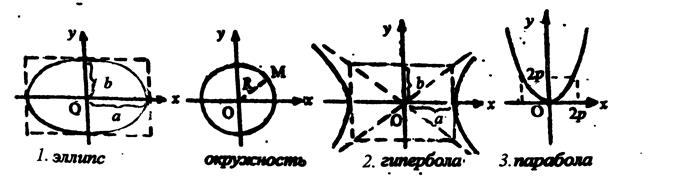
Плоские линии второго порядка.

Линиявторого порядка на плоскости удовлетворяет уравнению второй степени общего вида

a ₁₁ x ² +2 a ₁₂ x y + a ₂₂ y ² + b ₁ x + b ₂ y + c = 0, (16)

где хотя бы один из коэффициентов a ₁₁, a ₁₂, a ₂₂ не равен нулю. Принято исключать

из рассмотрения т.наз. распадающиеся уравнения, когда левая часть в (16) является произведением двух выражений 1-й степени по x и y. Распадающиеся уравнения описывают либо одну прямую (например, уравнение x ² = 0), либо пару прямых (например, уравнение x × y = 0). Далее рассматриваются только нераспадающиеся уравнения, которым соответствуют искривленные линии.

С помощью поворота системы координат можно перейти к новым координатах, в

которых уравнение вида (16) упрощается, а именно, отсутствует слагаемое вида 2 a ₁₂ x y. Последующим сдвигом начала системы координат можно перейти к переменным, в которых уравнение линии еще более упрощается, а именно, отсутствует слагаемое вида b ₁ x или b ₂ y, либо отсутствуют оба таких слагаемых. В результате выясняется, что существуют лишь три класса линий с нераспадающимся уравнением второй степени: эллипс, гипербола и парабола. Для каждого из этих классов имеется простейшая стандартная форма уравнения, называемая канонической.

1.Эллипс: каноническое уравнение

x ² / a ² + y ² / b ² = 1 (a > 0, b > 0). (17)

Этот эллипс представляет собой овал, вписанный в прямоугольник со сторонами x = ± a, y = ± b. Центр данного эллипса совпадает с началом координат O, отрезки a и b называются полуосями эллипса (вдоль координатных осей O x и O y, соответственно), точки (± a; 0) и (0; ± b) называются вершинами эллипса. При

a = b = R эллипс переходит в окружность радиуса R с центром в начале координат O (уравнение такой окружности x ²+ y ²= R ² ).

Уравнение (x - x ₀)² / a ² + (y - y ₀)² / b ² = 1 есть каноническое уравнение эллипса с центром в точке M₀(x ₀; y ₀) и с полуосями a и b вдоль координатных осей.

2.Гипербола: каноническое уравнение

x ² / a ² - y ² / b ² = 1 (a > 0, b > 0). (18)

Эта гипербола состоит из двух сплошных линий (- связных компонент),

«описанных» около прямоугольника со сторонами x = ± a, y = ± b. Центр данной гиперболы совпадает с началом координат O, оси гиперболы совпадают с координатными осями, точки (± a; 0) называются вершинами гиперболы. Отрезок a (на оси O x) называется вещественной полуосью. Отрезок b (на оси O y) называется мнимой полуосью. Прямые y = ± (b / a)× x называются асимптотами гиперболы; к ним сколь угодно близко приближаются точки гиперболы при удалении от начала координат.

Уравнение (x - x ₀)² / a ² - (y - y ₀)² / b ² = 1 есть каноническое уравнение гиперболы с центром в точке M₀(x ₀; y ₀), вещественной полуосью a (в направлении оси O x) и с мнимой полуосью b (в направлении оси O y).Заметим, что часто встречающееся уравнение x × y = 1 (или y = 1 / x) есть также уравнение гиперболы, однако неканонического вида.

3.Парабола: каноническое уравнение

y = x ² / 2 p (p > 0). (20)

Вершина данной гиперболы - начало координат O, ветви направлены вверх.

уравнение y - y ₀ =(x - x ₀)² / 2 p есть уравнение параболы с вершиной M₀(x ₀; y ₀)и с ветвями вверх.