





Пусть имеются две точки М
1(
x 1,
y 1) и М
2(
x 2,
y 2). Из геометрических соображений (рис. 2) угловой коэффициент искомой прямой равен
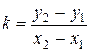
. Подставим полученное значение
k в уравнение (3):
y = 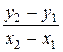 x +b
x +b.
Рис. 2 Учитывая, что прямая проходит через точку М1(x 1, y 1), а, значит, ее координаты удовлетворяют искомому уравнению прямой, находим
b= y 1 - 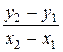 x 1.
x 1.
Окончательно уравнение прямой, проходящей через две заданные точки, записываем в виде
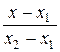 =
= 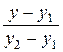 . (4)
. (4)
Пример 3. Составить уравнение прямой, проходящей через точки А(1,2) и В(-1,3).
Решение. Искомое уравнение, согласно (4), имеет вид 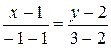 , откуда x + 2 y - 5 = 0. ■
, откуда x + 2 y - 5 = 0. ■






 Пусть имеются две точки М1(x 1, y 1) и М2(x 2, y 2). Из геометрических соображений (рис. 2) угловой коэффициент искомой прямой равен
Пусть имеются две точки М1(x 1, y 1) и М2(x 2, y 2). Из геометрических соображений (рис. 2) угловой коэффициент искомой прямой равен 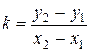 . Подставим полученное значение k в уравнение (3): y =
. Подставим полученное значение k в уравнение (3): y = 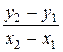 x +b.
x +b.

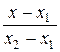 =
= 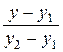 . (4)
. (4)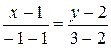 , откуда x + 2 y - 5 = 0. ■
, откуда x + 2 y - 5 = 0. ■


