Задача 4. Использование условия параллельности двух прямых.
Признаком параллельности двух прямых является равенство их угловых коэффициентов k 1= k 2, так как у параллельных прямых углы наклона к оси абсцисс одинаковы. Замечание. Если прямые заданы общими уравнениями A 1 x + B 1 y + C 1=0 и A 2 x + B 2 y + C 2=0, то вместо формулы (5) для вычисления угла j между этими прямыми можно пользоваться формулой:
Из формулы (6) видно, что необходимое и достаточное условие перпендикулярности двух прямых в этом случае имеет вид А 1 А 2+ В 1 В 2 = 0, а условием параллельности является равенство Пример 7. Составить уравнение прямой, проходящей через точку М0(1,-3) параллельно прямой y = 2 x - 20. Решение. В искомом уравнении прямой y=kx+b угловой коэффициент k равен 2. Учитывая, что прямая проходит через точку М0, находим b: -3 = 2×1 + b; b = -5. Искомое уравнение прямой y = 2 x - 5. ■
|

 =
= 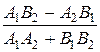 . (6)
. (6)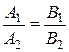 .
.


