Плоскость и прямая в пространстве.
3.1. Уравнение поверхности в пространстве. Положение точки в пространстве определяется тремя координатами. Прямоугольная декартова система координат в пространстве представляет собой три перпендикулярные прямые Ox, Oy, Oz, снабженные масштабами и направлениями. Такие прямые называются координатными осями. Координатами точки M 0(x 0 ,y 0 ,z 0) называются координаты оснований перпендикуляров, опущенных из этой точки на координатные оси. Уравнением поверхности (в выбранной системе координат) называется такое уравнение с тремя переменными F (x,y,z)=0, которому удовлетворяют координаты каждой точки, лежащей на этой поверхности, и только они. 3.2. Плоскость в пространстве. Пусть плоскость проходит через точку M 0(x 0 ,y 0 ,z 0) перпендикулярно вектору
скалярное произведение этих векторов равно нулю, т.е. (
  Уравнение (18) представляет уравнение плоскости, перпендикулярной данному вектору Уравнение (18) представляет уравнение плоскости, перпендикулярной данному вектору  = (А,B,C) и проходящей через данную точку M 0(x 0 ,y 0 ,z 0) (рис. 9). = (А,B,C) и проходящей через данную точку M 0(x 0 ,y 0 ,z 0) (рис. 9).
    Пример 16. Составить уравнение плоскости, проходящей через точку M 0(-1,0,2) и перпендикулярной вектору Пример 16. Составить уравнение плоскости, проходящей через точку M 0(-1,0,2) и перпендикулярной вектору  = (2,5,-1). = (2,5,-1).
Решение. Искомое уравнение имеет вид 2(x+ 1)+5(y- 0)-1(z- 2)=0. ■ Уравнение плоскости, записанное в виде Аx + By + Cz + D = 0 (19) (где D = - Аx 0 - By 0 - Cz 0), называется общим уравнением плоскости. Так, в предыдущем примере уравнению можно придать вид 2 x+ 5y-z+4 = 0. Замечание. Всякое уравнение вида (19) (где хотя бы одно из чисел А, В, С не равно нулю) задает плоскость в пространстве и, наоборот, уравнение любой плоскости есть уравнение первой степени. Отметим, что уравнение ( ( что приводит к уравнению плоскости в форме определителя:
В частности, если плоскость не проходит через начало координат и пересекает координатные оси в точках M 1 (a,0,0), M 2 (0, b,0), M 3 (0,0, c), то уравнение (20) приводится к виду
называемому уравнением плоскости «в отрезках». Рассмотрим далее частные случаи общего уравнения плоскости. Если D= 0, то уравнение Аx+By+Cz= 0 определяет плоскость, проходящую через начало координат. Другие частные случаи определяются расположением нормального вектора Двугранный угол между двумя плоскостями, заданными своими общими уравнениями А 1 x + B 1 y + C 1 z + D 1 = 0, А 2 x + B 2 y + C 2 z + D 2 = 0, (22) равен углу j между их нормальными векторами cos j = угол j лежит в пределах от 0 до p; другой двугранный угол, образованный двумя пересекающимися плоскостями, равен p - j. Пример 17. Найти угол между плоскостями, заданными уравнениями 3 x-y- 2 z +250 = 0 и x -2 y+z -111 = 0. Решение. Находим косинус угла между нормальными векторами cos j = отсюда j=arccos Две данные плоскости (22) перпендикулярны тогда и только тогда, когда их нормальные векторы Пример 18. Составить уравнение плоскости, проходящей через точку M 0(1,-1,0) и параллельной плоскости 2 x +3 y- 4 z -1 = 0. Решение. Так как у параллельных плоскостей один и тот же нормальный вектор
3.3 [кроме ФЭУ] .Прямая линия в пространстве. Линия в пространстве определяется совместным заданием двух уравнений F (x,y,z)=0, F (x,y,z)=0 как пересечение двух поверхностей, задаваемых этими уравнениями. Так, прямая в пространстве может быть задана как линия пересечения двух плоскостей, т.е. как множество точек, удовлетворяющих системе Если прямая в пространстве параллельна вектору
Уравнения (24) называются каноническими уравнениями прямой в пространстве. Пример 19. Составить уравнения прямой, проходящей через точки M 0(1,-1,3) и M 1(0,3,5). Решение. Воспользуемся уравнениями (24), взяв в качестве направляющего вектора
|

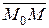 = (x-x 0, y-y 0, z-z 0) и
= (x-x 0, y-y 0, z-z 0) и  ,
, 
 А (x- x 0) + В (y- y 0) + C (z- z 0) = 0. (18)
А (x- x 0) + В (y- y 0) + C (z- z 0) = 0. (18)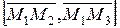 - векторное произведение
- векторное произведение  на
на 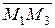 , а в качестве M 0 точку M 1, получим
, а в качестве M 0 точку M 1, получим ) = 0,
) = 0, . (20)
. (20) , (21)
, (21) =(А 1 ,B 1 ,C 1) и
=(А 1 ,B 1 ,C 1) и 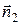 = =(А 2 ,B 2 ,C 2) и определяется по формуле
= =(А 2 ,B 2 ,C 2) и определяется по формуле =
= 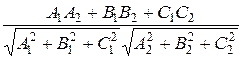 ; (23)
; (23)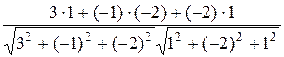 =
=  ;
;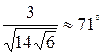 . Другой двугранный угол равен 180°-71°=109°. ■
. Другой двугранный угол равен 180°-71°=109°. ■ =0. Например, плоскости 3 x - y +2 z -31 = 0 и 5 x+ 3 y -6 z +1 = 0 перпендикулярны, так как 3×5+(-1) ×3+2×(-6)=0. Две данные плоскости параллельны тогда и только тогда, когда их нормальные векторы
=0. Например, плоскости 3 x - y +2 z -31 = 0 и 5 x+ 3 y -6 z +1 = 0 перпендикулярны, так как 3×5+(-1) ×3+2×(-6)=0. Две данные плоскости параллельны тогда и только тогда, когда их нормальные векторы 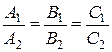 .
.
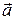 = (а 1, а 2, а 3) (называемому направляющим вектором) и проходит через точку M 0(x 0 ,y 0 ,z 0), то её уравнения могут быть получены из условия коллинеарности векторов
= (а 1, а 2, а 3) (называемому направляющим вектором) и проходит через точку M 0(x 0 ,y 0 ,z 0), то её уравнения могут быть получены из условия коллинеарности векторов 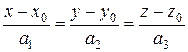 . (24)
. (24)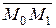 = (0-1,3-(-1),5-3) или
= (0-1,3-(-1),5-3) или 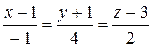 .
.


