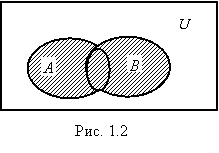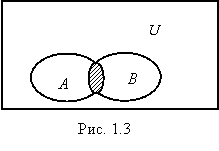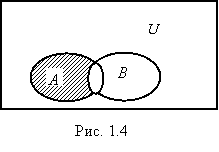Пустое и универсальное множества
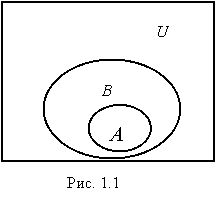
Определение 1.1. В теории множеств отдельно вводится множество, которое не содержит ни одного элемента. Такое множество называется пустым и обозначается символом Æ. В любой конкретной задаче приходится иметь дело только с подмножествами некоторого, фиксированного для данной задачи, множества. Его принято называть универсальным и обозначать символом U. Например, при сборке некоторого изделия универсальным множеством естественно назвать множество всех деталей и сборочных элементов, из которых это изделие состоит. Если мы рассматриваем множества, связанные с какими-нибудь фигурами на плоскости, то в качестве универсального множества можно выбрать множество всех точек плоскости. Определение 1.2. Два множества A и B называются равными (A = B), если они состоят из одних и тех же элементов. Поэтому несуществен порядок записи в фигурных скобках элементов множества, задаваемого списком, т.е. { a, b, c } = { a, c, b }. Определение 1.3. Множество A называется подмножеством множества B, если любой элемент множества A принадлежит множеству B. При этом пишут A Ì B, где " Ì " есть знак вложения подмножества. Из определения следует, что для любого множества A справедливы, как минимум, два вложения A Ì A и A Ì U. Определение 1.4. Если A Ì B и A ¹ B, A ¹ Æ, то A называется собственным подмножеством множества B. В этом случае B содержит хотя бы один элемент, не принадлежащий A. В теории множеств, по определению, полагают, что пустое множество является подмножеством любого множества: Æ ÌA. Пустое множество и само множество A называются несобственными подмножествами множества A. При графическом изображении множеств удобно использовать диаграммы Венна, на которых универсальное множество обычно представляют в виде прямоугольника, а остальные множества в виде овалов, заключенных внутри этого прямоугольника (рис 1.1).
Определение 1.5. Объединением множеств A и B (обозначение A ÈB) называется множество элементов x таких, что x принадлежит хотя бы одному из двух множеств A или B (рис 1.2). Символически это можно записать следующим образом: AÈ B = {x|x Î A или x Î B}.
Определение 1.6. Пересечением множеств A и B (обозначение A ÈB) называется множество, состоящее из элементов x, которые принадлежат и множеству A и множеству B (рис. 1.3): AÈ B = { x|x Î A и x Î B}.
Определение 1.7. Разностью множеств A и B называется множество всех тех элементов множества A, которые не принадлежат множеству B (рис. 1.4): A\B = { x|x Î A и x Î B}.
Определение 1.8. Симметрической разностью множеств A и B называется множество A D B = (A\B) È (B\A) (рис. 1.5).
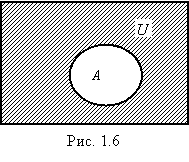
Определение 1.9. Абсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, т.е. множество A = U\A, где U - универсальное множество (рис. 1.6).
В дальнейшем вместо термина "абсолютное дополнение" мы будем употреблять термин "дополнение". Пример 1.1. Если U = { a, b, c, d, e, f, g, h }, A = { c, d, e }, B = { a, c, e, f, h }, то
|