Геометрические векторы.
Геометрический вектор - это направленный отрезок в пространстве. Обозначается: Прямоугольные системы координат O xyz в трехмерном пространствебывают левые (например, оси: O x вправо, O y вперед, O z вверх) и правые (например, оси:O x вперед, O y право, O z вверх). Правая система не совмещается с левой поворотами (системы как целого) в пространстве. Каждая точка M пространства имеет три координаты (числа), которые записываются в скобках после обозначения точки: M(x;y;z).Например, чтобы изобразить точку M(-2;3;4), следует из начала координат O переместиться на 2 единицы в направлении, противоположном оси O x, затем на 3 единицы в направлении оси O y и на 4 единицы вверх; в результате мы попадем в точку M. Соответственно, каждый геометрический вектор характеризуется тремя координатами x, y, z - числовыми проекциями вектора на координатные оси. Координаты записывают в скобках после обозначения вектора: x = x 2- x 1, y = y 2- y 1, z = z 2- z 1. (1) Ортами прямоугольной системы координат называются три вектора
Формула (2) устанавливает взаимно однозначное соответствие между геометрическими векторами Пример. (а) Координатысередины (центра масс, центра тяжести) K отрезка равны полусуммам одноименных координат точек A1 и A2. (б) В треугольнике A1A2A3 координаты точки пересечения медиан (центра масс, центра тяжести) K равны средним арифметическим значениям одноименных координат вершин. (в) Втреугольнойпирамиде A1A2A3A4 координаты центра масс (центра тяжести) K равны средним арифметическим значениям одноименных координат вершин пирамиды. · Пояснение. (а) Очевидно, в координатах, получим xK - x1 = 1/2×(x 2 – x 1), откуда x K= 1/2×(x 1 + x 2); аналогично находятся y K, z K. (б) Пусть A1B - медиана, x B = 1/2×(x 2+ x 3). Как известно, точка K делит медиану A1B на отрезки в отношении 2:1 по длине (считая от вершины A1). Тогда
|

 , где A1 и A2 - начальная и конечная точки вектора. Абстрактное обозначение вектора:
, где A1 и A2 - начальная и конечная точки вектора. Абстрактное обозначение вектора:  и т.д. Механический смысл вектора
и т.д. Механический смысл вектора  (x; y; z).Зная координаты начальной и конечной точек A1(x 1; y 1; z 1) и A2(x 2; y 2; z 2) вектора
(x; y; z).Зная координаты начальной и конечной точек A1(x 1; y 1; z 1) и A2(x 2; y 2; z 2) вектора  длины 1 вдоль координатных осей (ед. число - орт; слово ortho означает «прямой»). Орты образуют базис в трехмерном пространстве, так как любой вектор
длины 1 вдоль координатных осей (ед. число - орт; слово ortho означает «прямой»). Орты образуют базис в трехмерном пространстве, так как любой вектор 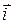 + y ×
+ y ×  + z ×
+ z × 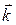 . (2)
. (2)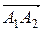
 = 1/2 ×
= 1/2 ×  . Расписывая это равенство в координатах, получим x K - x 1 =2/3×(x B- x 1), откуда x K= x 1+2/3× x B-2/3× x 1= x 1+ 2/3×1/2×(x 2+ x 3) - 2/3× x 1=(x 1+ x 2+ x 3)/3. Для y K и z K выражения аналогичны. (в) Пусть D - точка пересечения медиан треугольника A1A2A3, тогда x D=1/3×(x 1+ x 2+x3). Точка K находится на отрезке A4D и делит его на части в отношении 3:1 по длине (считая от вершины A4).Тогда
. Расписывая это равенство в координатах, получим x K - x 1 =2/3×(x B- x 1), откуда x K= x 1+2/3× x B-2/3× x 1= x 1+ 2/3×1/2×(x 2+ x 3) - 2/3× x 1=(x 1+ x 2+ x 3)/3. Для y K и z K выражения аналогичны. (в) Пусть D - точка пересечения медиан треугольника A1A2A3, тогда x D=1/3×(x 1+ x 2+x3). Точка K находится на отрезке A4D и делит его на части в отношении 3:1 по длине (считая от вершины A4).Тогда  =3/4×
=3/4×  . Расписывая это равенство в координатах, получим x K- x 4= 3/4 × (x D- x 4), откуда x K= x 4 +3/4× 1/3 ×(x 1+ x 2+ x 3) - 3/4× x 4 = (x 1+ x 2+ x 3+ x 4) /4. ·
. Расписывая это равенство в координатах, получим x K- x 4= 3/4 × (x D- x 4), откуда x K= x 4 +3/4× 1/3 ×(x 1+ x 2+ x 3) - 3/4× x 4 = (x 1+ x 2+ x 3+ x 4) /4. ·


