Определители
Для каждой квадратной матрицы определено число, называемое определителем матрицы, детерминантом матрицы или просто определителем (детерминантом). Определение. Определителем квадратной матрицы первого порядка называется число, равное единственному элементу этой матрицы: A={a}, detA=|A|=a. Пусть A — произвольная квадратная матрица порядка n, n>1:
Определение Определителем n-го порядка (определителем квадратной матрицы n-го порядка n), n>1, называется число, равное
где Для определителей 2-го и 3-го порядка легко получить простые выражения через элементы матрицы. Определитель 2-го порядка:
Определитель 3-го порядка:
2.1. Минор и алгебраическое дополнение элемента Определение. Минором элемента матрицы называется определитель матрицы, полученной вычеркиванием строки и столбца, в которых расположен элемент. Обозначаем: минор элемента aij — Определение. Алгебраическим дополнением элемента матрицы называется его минор, умноженный на -1 в степени, равной сумме номеров строки и столбца, в которых расположен элемент. Обозначаем: алгебраическое дополнение элемента aij — Таким образом можно переформулировать определение определителя n-го порядка: определитель n-го порядка, n>1, равен сумме произведений элементов первой строки на их алгебраические дополнения.
|

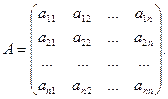

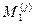 — определитель квадратной матрицы полученной из матрицы A вычеркиванием превой строки и j-го столбца.
— определитель квадратной матрицы полученной из матрицы A вычеркиванием превой строки и j-го столбца. .
. .
. .
. .
.


