Численные примеры решенные вручную

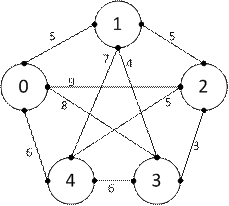
Пример 1.

Дан граф:

Найти на нем путь минимальной длины.

Решим задачу методом ветвей и границ.

Составим для графа матрицу переходов:

0	X
		X
			X
				X
					X

Коэффициент приведения по строке находятся как сумма минимальных элементов в строке. т.е. K1=5+4+3+3+5=20.

Приведение по строкам выполняется путем вычитания из каждого элемента минимального для данной строки. После приведения по строкам матрица примет вид:

0	X
		X
			X
				X
					X

Коэффициент приведения по столбцу находится как сумма минимальных элементов каждого столбца, т.е. K2=1+0+0+0+1=2.

Приведение по столбцам выполняется путем вычитания из элементов матрицы минимального для данного столбца. После приведения матрица примет вид:

0	X
		X
			X
				X
					X

Нижняя граница вычисляется как сумма коэффициентов приведения по строке и по столбцу. Гн=K1+K2=22.

При этом верхняя граница Гв=22.

Сократим матрицу путем удаления 0-й строки и первого столбца с минимальным значением в 0-й строке. Матрица примет вид:

1
		X
			X
				X

Коэффициент приведения по строкам K1=0, поэтому приведение по строкам делать не нужно. Коэффициент приведения по столбцам K2=1, поэтому необходимо выполнить приведение по столбцам, после чего матрица примет вид:

1
		X
			X
				X

Гв=23.

Теперь сократим матрицу путем удаления столбца с минимальным значением в 1-й строке. При этом нулевой столбец удалять нельзя. Также уделяется сама 1-я строка. После этого матрица будет иметь вид:

		X
3
			X

Как видно, K1=0 и K2=0. Поэтому матрица уже является приведенной.

Сократим матрицу путем удаления столбца с минимальным значением в 3-й строке, при этом удаление 0-го столбца запрещено. Также удаляется сама 3-я строка. Матрица принимает вид:

2
		X

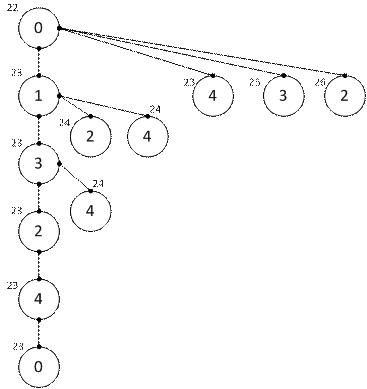
Матрица является приведенной.

Гв=23.

Сократим матрицу путем удаления 4-го столбца и 2-й строки:

Теперь остался всего один переход.

Гв=23.

Таким образом, в ходе выполнения алгоритма была пройдена только одна ветвь, длина пути которой равна 23.

В ходе работы строилось дерево переходов:

Дальнейшая работа алгоритм заключается в проходе других оставшихся ветвей, игнорируя при этом те ветви, длина пути которых больше, чем минимальная верхняя граница. В результате можно получить следующее дерево обхода:

Видно, что минимальной будет длина 23, найденная при проходе первой ветви.

Пример 2.

Дан граф:

Матрица переходов для него будет иметь вид:

	X		X
		X		X		X
	X		X
		X		X	X
				X	X
		X				X

Гн=26.

При обходе всех ветвей будет составлено дерево вида:

Видно, что минимальная длина пути – 28.