Решение. Будем считать, что агента 1 - это игрок А, а агент 2 – игрок В.
Будем считать, что агента 1 - это игрок А, а агент 2 – игрок В. Стратегии агента 1: А1 – кооперироваться, А2 – не кооперироваться. Стратегии агента 2: В1 – кооперироваться, В2 – не кооперироваться.
На первом этапе решения задачи нужно определить: решается ли поставленная задача в чистых стратегиях. Для этого найдем нижнюю и верхнюю цены игры:
α ≠ β;, седловая точка отсутствует. Следовательно, оптимальное решение игры следует искать в смешанных стратегиях игроков: S* A = (p* 1 , p* 2 ) и S* B = (q* 1 , q* 2 ) Игра имеет размер 2 × 2. Поэтому игру можно решить графическим способом.
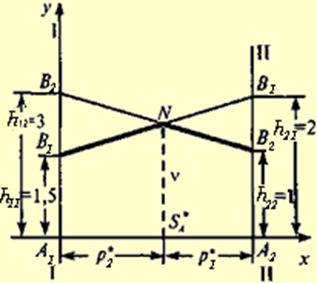
Второй этап: решение игры в смешанных стратегиях геометрическим способом. Решение игры геометрическим методом состоит из двух шагов: 1. определение оптимальной стратегии игрока А, 2. определение оптимальной стратегии игрока В Шаг 1. Оптимальная стратегия игрока А S*A=(p*1p*2), в соответствии с принципом минимакса, определяется координатами точки пересечения двух прямых, соответствующих стратегиям В1 и В2 игрока В, в которой минимальный выигрыш игрока А достигает максимума. Ордината этой точки равна цене игры v. Построим геометрическую модель игры. По оси абсцисс (рисунок 1) откладываем единичный отрезок A1A2. Ось I-I соответствует выбору игроком А стратегии A1, ось II—II - стратегии A2. На вертикальной оси I-I откладываем отрезки: h11=1,5, соответствующий стратегии B1, и h12 = 3, соответствующий стратегии B2 – выигрыши игрока А при выборе им стратегии А1. На вертикальной оси II—II отрезок h21=2 соответствует стратегии B1 , отрезок h22=1 соответствует стратегии B2 (рисунок 1) – при выборе игроком А стратегии A2. Нижняя цена игры α=h11=1,5. Верхняя цена игры β =h21=2. На графике видно, что седловая точка отсутствует (α ≠β). Абсцисса точки N – точки пересечения прямых B1B1 и B2B2, определяет оптимальную стратегию S*A, а ордината - цену игры v.
Рисунок 1 – Графическое решение игры для игрока А
Определим уравнения прямых B1B1 и B2B2. Уравнение прямой, проходящей через две точки, имеет вид:
Следовательно, уравнение прямой B1B1, проходящей через точки (0; 1,5) и (1; 2), будет
Уравнение прямой B2B2, проходящей через точки (0; 3) и (1; 1):
Тогда, точка пересечения этих прямых является решением системы:
Таким образом, p*2=0,6, p*1=1-0,6=0,4; цена игры v =1,8; Оптимальная стратегия S*A = (0,4;0,6),
Шаг 2. Оптимальную стратегию игрока В геометрически можно определить, если поменять местами игроков А и В и вместо максимума нижней границы A2MA1 в соответствии с принципом минимакса рассмотреть минимум верхней границы. Абсцисса точки М определяет q*2 в оптимальной стратегии игрока В, ордината этой точки - цена игры. Прямая A1A1, проходящая через точки (0; 1,5) и (1; 3), удовлетворяет уравнению y = 1,5x + 1,5. Прямая A2A2, проходящая через точки (0; 2) и (1; 1), удовлетворяет уравнению у = - х +2.
Рисунок 2 – Графическое решение игры для игрока В
Координаты их точки пересечения М- это решение системы уравнений:
Откуда x=0,2; y=1,8, т.е. М(0,2;1,8) q*2=0,2, q*1=1-q*2 =0,8, v =y=1,8, Оптимальная стратегия S*B = (0,8;0,2)
Ответ:
игра решена в смешанных стратегиях. Цена игры равна 1,8. Оптимальное решение игры:
|
или y = 0,5x + 1,5.
или y = -2x + 3.
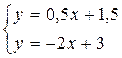или x=0,6; y =1,8, т.е. N(0,6; 1,8)
.
, 
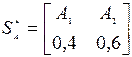, т.е. при взаимодействии с оппонентом агент 1 должен на 40% применять стратегию кооперации и на 60% некооперации с оппонентом, а агент 2 должен кооперироваться с оппонентом в 80% случаев и не кооперироваться – в 20%.
