Идеальные и неидеальные смеси
В зависимости от взаимной растворимости компонентов различают смеси жидкостей: 1) с неограниченной взаимной растворимостью; 2) взаимно нерастворимых; 3) ограниченно растворимых друг в друге. Смеси с неограниченной взаимной растворимостью компонентов в свою очередь делятся на идеальные и неидеальные смеси с положительным или отрицательным отклонением от закона Рауля. Идеальными называются смеси, компоненты которых при смешении не изменяют объема, а само смешение происходит без тепловых эффектов. Идеальные смеси подчиняются закону Рауля. Соответственно неидеальными считаются смеси, имеющие отклонения от закона Рауля. Согласно закону Рауля, парциальное давление каждого компонента в паре пропорционально мольной доле этого компонента в растворе. Например, для низкокипящего компонента А:
При этом в качестве коэффициента пропорциональности в уравнении выступает давление насыщенного пара Согласно закону Дальтона, для идеальной газовой смеси общее давление пара над раствором равно сумме парциальных давлений его компонентов. Для бинарной смеси
Для парциальных давлений компонентов можно также записать:
В соответствие с законом Рауля и Дальтона общее давление паровой
Из уравнения (3.1) следует, что при постоянной температуре парциальные давления компонентов, а также общее давление паров над смесью находятся в линейной зависимости от мольной доли
Рис. 3.1. Изотермы парциальных давлений компонентов и общего давления для идеальных растворов (диаграмма
В условиях равновесия
откуда следует
Обычно процесс ректификации проводят при общем постоянном давлении Решим второе уравнение (3.2) относительно
получим
При известных значениях Согласно правилу фаз Гиббса
получим для бинарной смеси С = 2 (Ф = 2, К = 2), т. е. равновесную зависимость графически можно получить, используя две переменные величины (Р и х, Т и х, Р и Т, х и у). При
Рис. 3.2. Зависимость температур кипения и конденсации от состава фаз (диаграмма
Нижняя ветвь на диаграмме Т – х,у будет отвечать температурам кипения жидкой смеси, верхняя – температурам конденсации паровой фазы. Располагая этой диаграммой, можно по составу жидкой фазы х1 найти равновесный ей состав пара у1 и температуру в системе Т1. Для анализа процессов ректификации более удобна диаграмма у – х, построенная на основе диаграммы Т – х,у (рис. 3.3).
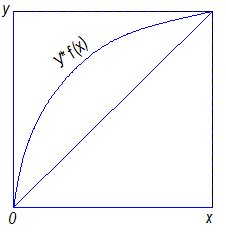
Рис. 3.3. Диаграмма равновесия пар-жидкость (диаграмма
Кривая равновесия в этой диаграмме отвечает уравнению
Если ввести отношение
Величины
где Следует отметить, что изменение давления существенно влияет на положение равновесной зависимости Взаимное положение кривых на фазовых диаграммах определяется первым законом Коновалова: пар обогащается тем компонентом, при добавлении которого к жидкости повышается давление пара над ней или снижается ее температура. Первый закон Коновалова дополняется первым законом Вревского, указывающим как влияет температура и соответственно давление на равновесные составы фаз: при повышении температуры смеси испаряется преимущественно тот компонент, парциальная мольная температура испарения которого больше, что обуславливает относительно большее содержание этого компонента в паре.
Рис. 3.4. Расположение линий равновесия в диаграмме в зависимости от давления
Для идеальной смеси, состоящей их нескольких компонентов, уравнения, связывающие равновесные концентрации, могут быть получены так же, как и для идеальной бинарной смеси. Для жидкой смеси, состоящей из n компонентов на основе законов Рауля и Дальтона имеем:
Общее давление в системе равно
Для j -го компонента в состоянии равновесия получим
введя относительные летучести компонентов
Для неидеальной паровой и жидкой фаз уравнение равновесия можно записать в виде
где Вместо давления насыщенного пара чистого компонента вводится активность При умеренных давлениях (р < 10 МПа) активность
Чтобы использовать это уравнение для расчета равновесных составов, необходимо для каждого компонента знать коэффициент активности
Величины Таким образом, для неидеальных смесей кривая равновесия может быть рассчитана только по известным коэффициентам активности, определение которых весьма затруднительно. Поэтому в большинстве случаев диаграммы В случае полной нерастворимости компонентов смеси силы взаимодействия между молекулами этих компонентов отсутствуют и каждый компонент ведет себя независимо друг от друга. В этом случае бинарная смесь закипает при давлении
При нерастворимости компонентов парциальное давление каждого компонента равно давлению насыщенного пара при той же температуре. Температура кипения смеси остается постоянной независимо от состава жидкой смеси
Рис. 3.5. Диаграммы
Так как в природе нет абсолютно нерастворимых друг в друге веществ, в интервалах незначительной растворимости одного компонента в другом температуры кипения компонентов будут меняться по линиям
На основе диаграммы Т – х, у можно построить равновесную зависимость в координатах Для частично растворимых смесей линия постоянных температур уже (рис. 3.6, а). В отличие от идеального раствора, для которого коэффициенты активности равны единице, реальные хорошо растворимые жидкие смеси могут иметь положительные ( Для ряда смесей количественные отклонения от закона Рауля настолько велики, что приводят к качественно новым свойствам смесей. При некотором составе эти смеси имеют постоянную температуру кипения. При этой температуре состав равновесного пара над смесью равен составу жидкости (
а) б) в) Рис. 3.6. Фазовые диаграммы частично растворимых и азеотропных смесей: а) частично растворимая; б) с минимумом температуры кипения; в) с максимумом температуры кипения.
|

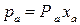 ,
, компонента А при соответствующей температуре.
компонента А при соответствующей температуре. .
. ;
;  .
.

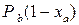 . (3.1)
. (3.1) низкокипящего компонента
низкокипящего компонента 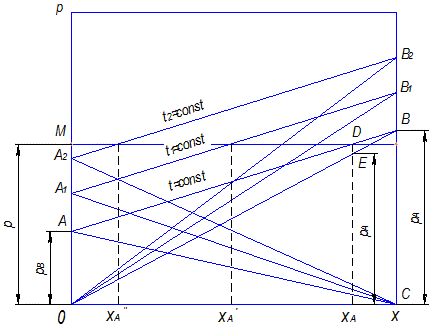
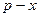 )
)
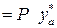 ;
; 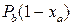
 ,
,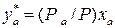 или
или 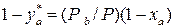 . (3.2)
. (3.2) .
. :
: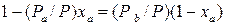 ,
, . (3.3)
. (3.3) и
и  в пределах температур кипения
в пределах температур кипения 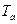 и
и  по уравнению (3.3) можно найти значения
по уравнению (3.3) можно найти значения  .
. ,
,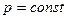 равновесную зависимость можно представить в координатах Т – х или у – х. Зная температуры и располагая значениями рассчитанных величин х и у, построим диаграмму, характеризующую равновесие в системе. Графики Т – у и Т – х при этом можно совместить (рис. 3.2).
равновесную зависимость можно представить в координатах Т – х или у – х. Зная температуры и располагая значениями рассчитанных величин х и у, построим диаграмму, характеризующую равновесие в системе. Графики Т – у и Т – х при этом можно совместить (рис. 3.2).
 ).
).
 ).
).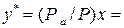


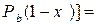

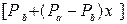 .
. , называемое относительной летучестью компонента А, то
, называемое относительной летучестью компонента А, то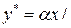
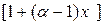 . (3.4)
. (3.4) и
и 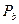 не являются постоянными в диапазоне температур кипения чистых компонентов
не являются постоянными в диапазоне температур кипения чистых компонентов  ,
, и
и  – относительные летучести при
– относительные летучести при  . С увеличением давления равновесная кривая располагается ближе к диагонали (рис. 3.4).
. С увеличением давления равновесная кривая располагается ближе к диагонали (рис. 3.4).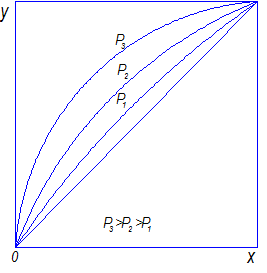
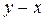
 ;
;  ;
; 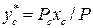 ;…….
;……. 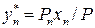 .
.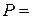




 .
. ,
,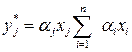 .
.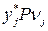
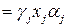 ,
, – поправка на неидеальность паровой фазы;
– поправка на неидеальность паровой фазы; 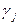 – поправка на неидеальность жидкой фазы.
– поправка на неидеальность жидкой фазы. (зависит от давления и температуры).
(зависит от давления и температуры).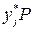
 .
.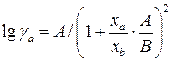 ;
;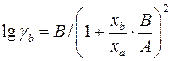 .
.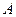 и
и 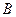 являются постоянными. Их значения приближенно можно рассчитать на основе знания некоторого минимума данных по равновесию. Располагая значениями равновесных концентраций в нескольких точках и значениями коэффициентов активности, можно найти постоянные
являются постоянными. Их значения приближенно можно рассчитать на основе знания некоторого минимума данных по равновесию. Располагая значениями равновесных концентраций в нескольких точках и значениями коэффициентов активности, можно найти постоянные 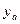 и после этого построить кривую равновесной зависимости.
и после этого построить кривую равновесной зависимости.
 для реальных растворов строятся на основе опытных данных.
для реальных растворов строятся на основе опытных данных.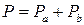 .
. на рис. 3.5).
на рис. 3.5).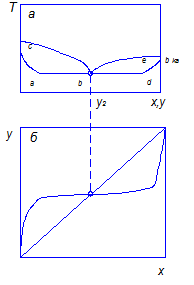
 взаимно нерастворимых жидкостей
взаимно нерастворимых жидкостей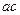 и
и  до температур кипения основных компонентов смеси. В областях растворимости будет происходить плавное изменение температур конденсации пара по линиям
до температур кипения основных компонентов смеси. В областях растворимости будет происходить плавное изменение температур конденсации пара по линиям  и
и 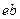 . В точке
. В точке  будет конденсироваться пар состава
будет конденсироваться пар состава  , причем значение этой величины равно
, причем значение этой величины равно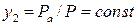 .
. ) и отрицательные (
) и отрицательные ( ) отклонения от закона Рауля. Для смесей с положительным отклонением линии парциальных давлений компонентов, а также линия общего давления проходят выше прямой линии для идеального раствора, тепло при растворении компонентов смеси поглощается. При отрицательном отклонении равновесная линия располагается ниже прямой линии идеального раствора, тепло при растворении компонентов выделяется.
) отклонения от закона Рауля. Для смесей с положительным отклонением линии парциальных давлений компонентов, а также линия общего давления проходят выше прямой линии для идеального раствора, тепло при растворении компонентов смеси поглощается. При отрицательном отклонении равновесная линия располагается ниже прямой линии идеального раствора, тепло при растворении компонентов выделяется. ). Такие смеси называют азеотропными, или нераздельно кипящими. Постоянная температура кипения таких растворимых смесей может иметь ярко выраженные минимумы или максимумы (рис. 3.7, б, в).
). Такие смеси называют азеотропными, или нераздельно кипящими. Постоянная температура кипения таких растворимых смесей может иметь ярко выраженные минимумы или максимумы (рис. 3.7, б, в).



