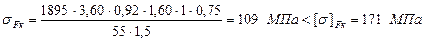Розв’язання. За табл. 2.2 вибираємо матеріали: для шестірні сталь 45, термообробка – покращення, твердість НВ230 (припускаємо
За табл. 2.2 вибираємо матеріали: для шестірні сталь 45, термообробка – покращення, твердість НВ230 (припускаємо, що діаметр заготовки менше 90 мм), границя текучості Базові межі контактної витривалості для шестірні і колеса (табл.2.3) відповідно:
Допустимий коефіцієнт безпеки для шестірні і колеса Число циклів навантаження зубів шестірні:
Число циклів навантаження зубів колеса:
де t – число годин роботи передачі за весь термін служби, тис. год; а – число зачеплень зуба за один оберт; а=1. Базове число циклів NH0 (табл.2.4): – для шестірні – для колеса Коефіцієнт довговічності КHL для шестірні і колеса приймаємо За формулою (2.1) визначаємо допустимі контактні напруження: – для шестірні:
– для колеса:
Для подальших розрахунків приймаємо допустиме напруження (формула 2.4):
Якщо Граничні допустимі контактні напруження для колеса, як менш міцного (оскільки
де Базові границі витривалості зубів на злам для шестірні і колеса (табл.2.5) відповідно:
Базові числа циклів зміни напруження шестірні і колеса (с.19):
Допустимий коефіцієнт безпеки для шестірні і колеса приймаємо Коефіцієнт довговічності для шестірні і колеса приймаємо Визначаємо допустимі напруження згину за формулою (2.5): – для шестірні:
– для колеса:
Граничні допустимі напруження згину: – для шестірні:
– для колеса:
При розрахунку зубчастої передачі візьмемо несиметричне розташування коліс відносно опор. Міжосьова відстань (формула 2.9):
де допоміжний коефіцієнт Ка=43 МПа1/3 (с. 21);
і=3,15 – передаточне відношення; КНβ=1 – коефіцієнт нервномірності навантаження по довжині зуба (примітка табл. 2.6); Ψba – коефіцієнт ширини колеса, визначається за формулою (2.10), в яку підставляємо значення коефіцієнта ширини колеса по діаметру
округлюємо до стандартного (с.21) і отримуємо Отримане значення аw округлюємо до ближчого стандартного значення (с. 22) і приймаємо аw=100 мм. Нормальний модуль зачеплення:
У відповідності з СТ СЭВ 310-76 (с. 22) приймаємо За формулою (2.12) визначаємо сумарне число зубів:
приймаємо Число зубів шістірні:
приймаємо Тоді число зубів колеса:
Визначаємо фактичне передаточне число:
Відхилення Δu значення фактичного передаточного числа від заданого передаточного відношення:
де За формулою (2.17) уточнюємо значення кута β;:
Основні розміри коліс: – діаметри ділильного кола: шестірні колеса Уточнюємо: – міжосьову відстань:
що дорівнює раніше прийнятому значенню міжосьової відстані; – діаметри вершин зубів: шестірні колеса – ширина вінця колеса – ширина шестірні Уточнюємо коефіцієнт ширини по діаметру шестірні:
Колова швидкість коліс (формула 2.24):
За табл. 2.7 при Сили, які діють в зачепленні (формули 2.27, 2.28, і 2.29): – колова:
– радіальна:
– oсьова:
За формулою (2.32) визначаємо розрахункові котактні напруження:
де
dш і bк – в мм;
Перевантаження складає:
що вище допустимого, тобто Збільшуємо ширину колеса: Уточнюємо коефіцієнт ширини колеса по діаметру:
Приймаємо
Визначаємо розрахункове напруження:
Перевантаження складає:
що менше допустимого, тобто Еквівалентне число зубів: – шестірні – колеса З таблиці 2.11 коефіцієнт форми зуба шестірні – для шістірні – для колеса Подальшу перевірку міцності проводимо для зубів колеса, як менш міцного, оскільки:
Перевіряємо зуби колеса на витривалість по напруженям згину за формулою (2.34):
де
Умова міцності виконується.
|

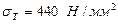 ;для колеса – сталь 45 термообробка – нормалізація, твердість НВ190, границя текучості
;для колеса – сталь 45 термообробка – нормалізація, твердість НВ190, границя текучості 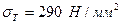 .
.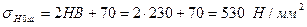 ;
;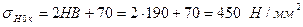 .
.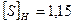 (с.18).
(с.18).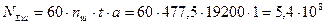 .
.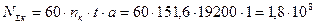 ,
,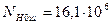 ;
;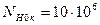 .
.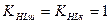 , оскільки
, оскільки 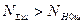 ,
, 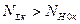 .
. ;
; .
.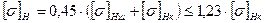 ,
,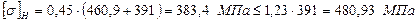 .
.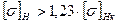 , то для розрахунків приймають
, то для розрахунків приймають 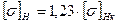 .
.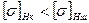 ):
):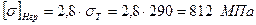 ,
, (табл.2.2) – границя текучості для матеріалу колеса.
(табл.2.2) – границя текучості для матеріалу колеса.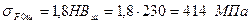 ;
;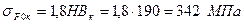 .
.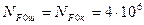 .
.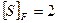 (с.19).
(с.19).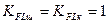 , оскільки
, оскільки 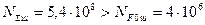 і
і 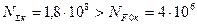 (
(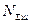 ,
, 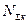 – с.35).
– с.35).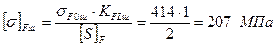 ;
;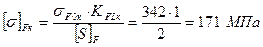 .
.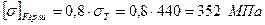 ;
;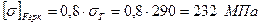 .
. ,
, – момент на валу шестірні, Н·мм:
– момент на валу шестірні, Н·мм: ;
;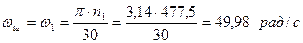 ;
; ;
;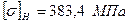 – допустимі контактні напруження;
– допустимі контактні напруження;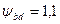 прийнятого з табл. 2.6 з урахуванням постійності навантаження і твердості <НВ 350:
прийнятого з табл. 2.6 з урахуванням постійності навантаження і твердості <НВ 350: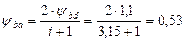 ,
,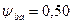 .
.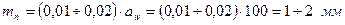 .
.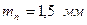 . Попередньо приймаємо кут нахилу зубів
. Попередньо приймаємо кут нахилу зубів 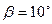 .
.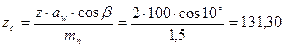 ,
,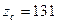 .
. ,
,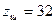 .
.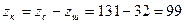 .
. .
.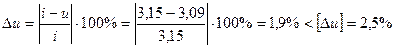 ,
,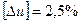 допустиме відхилення передаточного відношення (с. 22).
допустиме відхилення передаточного відношення (с. 22).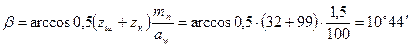 .
.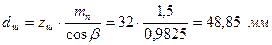 ;
;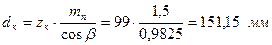 .
.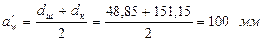 ,
,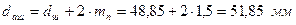 ;
;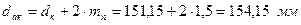 ;
;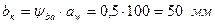 ;
;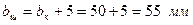 .
. .
.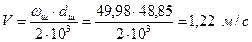 .
.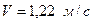 приймаємо 8-му степінь точності.
приймаємо 8-му степінь точності.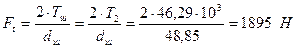 ;
;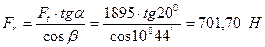 ;
;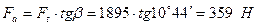 .
.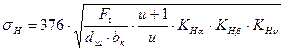 ,
,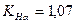 – коефіцієнт нерівномірного розподілу навантаження між зубами (табл. 2.9);
– коефіцієнт нерівномірного розподілу навантаження між зубами (табл. 2.9);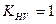 – коефіцієнт динамічності (табл. 2.8);
– коефіцієнт динамічності (табл. 2.8);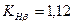 – коефіцієнт нервномірного розподілу навантаження по довжині зубів (з табл. 10 при
– коефіцієнт нервномірного розподілу навантаження по довжині зубів (з табл. 10 при 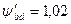 і несиметричному розміщенні коліс інтерполюванням знаходимо:
і несиметричному розміщенні коліс інтерполюванням знаходимо: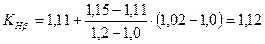 );
);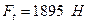 – колова сила;
– колова сила;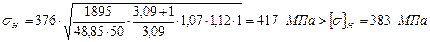 .
.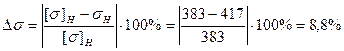 ,
,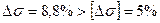 (с.25).
(с.25).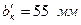 і шестірні:
і шестірні: 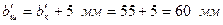 .
.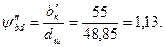
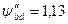 і несиметричному розташуванні коліс інтерполюванням знаходимо:
і несиметричному розташуванні коліс інтерполюванням знаходимо: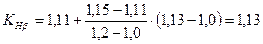 .
.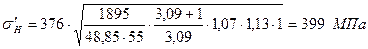 .
.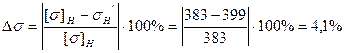 ,
,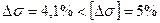 .
.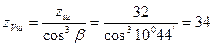 ;
;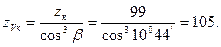
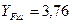 , колеса
, колеса 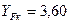 . Проводимо порівняльну оцінку міцності зубів на згин шляхом визначення відношення
. Проводимо порівняльну оцінку міцності зубів на згин шляхом визначення відношення 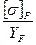 :
: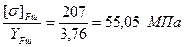 ;
;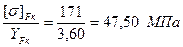 .
.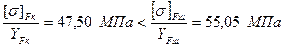 .
.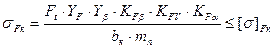 ,
,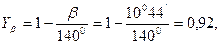 – коефіцієнт кута нахилу;
– коефіцієнт кута нахилу;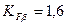 – коефіцієнт нерівномірності навантаження по довжині зубів (з табл. 2.12 при
– коефіцієнт нерівномірності навантаження по довжині зубів (з табл. 2.12 при 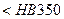 і несиметричному розташуванні коліс, інтнрполюванням знаходимо
і несиметричному розташуванні коліс, інтнрполюванням знаходимо 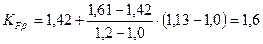 );
); – коефіцієнт динамічності (табл.2.13);
– коефіцієнт динамічності (табл.2.13); – коефіцієнт нерівномірності навантаження між зубами; при середньому значенні коефіцієнта торцевого перекриття
– коефіцієнт нерівномірності навантаження між зубами; при середньому значенні коефіцієнта торцевого перекриття 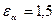 і 8 степені точності
і 8 степені точності 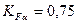 ;
;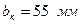 ,
,