Розрахунок параметрів циліндричної зубчастої передачі
З умови контактної міцності визначають міжосьову відстань передачі:
При цьому у формулу (2.8) підставляють не передаточне число передачі u, а передаточне відношення і, оскільки число зубів zш і zк невідомі і невідомо Тоді формула (2.8) має вигляд:
де Ka – коефіцієнт, що враховує форму суміжних зубів, механічні властивості матеріалу, степінь перекриття, розподіл навантаження між ланками і динамічність навантаження. Для стальних прямозубих коліс Тш – крутний момент на валу шестірні, Н мм; КНβ – коефіцієнт, який враховує нерівномірність розподілу навантаження по довжині зуба (табл. 2.6). При постійному навантаженні
де Для стандартних редукторів значення Ψba округлюють до стандартного значення з ряду: 0,125; 0,150; 0,160; 0,250; 0,315; 0,400; 0,500; 0,630; 0,800; 1,00; 1,25. Переважно Ψba приймають для прямозубих передач в межах 0,125…0,250; для косозубих – в межах 0,25…0,63. Таблиця 2.6. Значення Ψba, що рекомендується,
Отримане значення aw округлюють до стандартного значення по СТ СЭВ 229-75 (мм). Для стандартної передачі: ряд 1: 40; 50; 63; 80; 100; 125; 160; 200; 250; 315; 400; 500; 630; 800; ряд 2: 71; 90; 112; 140; 180; 224; 280; 355; 450; 560; 710; 900. Для нестандартної передачі aw округлюють до цілого числа. Вибирають модуль m з інтервалу (0,01…0,02)aw по ряд 1: 1; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; ряд 2: 1,25: 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14. Для косозубих коліс стандартний модуль – нормальний mn. Визначають сумарне число зубів – для прямозубих коліс:
– для косозубих коліс:
де β; – кут нахилу зубів, приймають mt – торцевий модуль, мм. Визначають число зубів шестерні zш і колеса zк:
Округлюють zш і zк до цілого числа. Визначають передаточне число:
Різниця з раніше прийнятим передаточним відношенням i повинно бути менше 2,5% при i ≤ 4,5 і 4% при i ≥ 4,5. Уточнюють міжосьову відстань aw за формулами: – для прямозубих передач:
– для косозубих передач:
Якщо значення
Якщо для косозубих передач у формулу (2.9) підставляють значення
При виконанні цієї умови в зачепленні знаходяться не менше двох пар зубів. Після визначення aw за формулою (2.9) можна задатися числом зубів zш з урахуванням умови
Значення модуля mn округлюють до стандартного значення. Визначають основні геометричні розміри шестірні і колеса: – діаметри ділильних кіл: для прямозубих коліс:
для косозубих коліс:
– діаметри вершин зубів: для прямозубих коліс:
для косозубих коліс:
– ширину вінця колеса: – ширину шестірні: – коефіцієнт ширини колеса по діаметру: – перевіряють, щоб уточнена міжосьова відстань Визначають колову швидкість коліс:
де ωш кутова швидкістьшестерні, рад/с, dш, мм. За табл.2.7 призначають степінь точності коліс. Розраховують сили, які діють в зачепленні: колова Ft, радіальна Fr і осьова Fa: – для прямозубої передачі:
– для косозубої передачі:
де α – кут зачеплення, в нормальних колесах β; – кут нахилу зубів. Таблиця 2.7. Степінь точності коліс
Визначають розрахункові контактні напруження
де ZH, ZM, Zε – коефіцієнти, що враховують відповідно форму зубів, механічні властивості матеріалу коліс, вплив коефіцієнта поперечного перекриття εα; для прямозубих коліс КНα – коефіцієнт розподілу навантаження між зубами; для прямозубих коліс КНβ – коефіцієнт нерівномірності навантаження по довжині зуба (табл. 2.6); КНν – коефіцієнт динамічності навантаження (табл. 2.8). Підставляючи у формулу (2.30) значення ZH, ZM, Zε отримують формули для визначення розрахункових контактних напружень: – для прямозубих передач:
– для косозубих передач:
де Ft – в Н; dш, bK – в мм; σн, [σ]Н – в МПа. Допускається перенавантаження Таблиця 2.8. Значення коефіцієнта КHV
Таблиця 2.9. Значення коефіцієнта КHα для косозубих і шевронних передач
Таблиця 2.10. Значення коефіцієнта КНβ
Визначають розрахункові напруження згину σ F в основі зуба шестірні і колеса за формулами: – для прямозубих передач:
– для косозубих передач:
де YF – коефіцієнт форми зуба, вибирають за табл. 2.11 в залежності від числа зубів z для прямозубих коліс і від числа зубів еквівалентних коліс zV для косозубих коліс; zV визначається за формулою:
Yβ – коефіцієнт кута нахилу зуба: – для прямозубої передачі – для косозубої передачі:
КFα – коефіцієнт, що враховує нерівномірність розподілу навантаження між зубами; – при значенні коефіцієнта осьового перекриття:
– при
де К – степінь точності передачі; εα – коефіцієнт поперечного перекриття:
при середньому значенні КFβ – коефіцієнт, що враховує нерівномірність розподілу навантаження по довжині зубів (табл. 2.12); KFV – коефіцієнт динамічності (табл. 2.13). Можна знаходити напруження згину лише для менш міцного колеса, яке визначають порівнюючи характеристики міцності зубів шестірні Тут Якщо
Таблиця 2.11. Коефіцієнт форми зуба YF
Таблиця 2.12. Значення коефіцієнта КFβ
Таблиця 2.13. Орінтовне значення коефіцієнта КFV
|

 , [мм]. (2.8)
, [мм]. (2.8) .
. , [мм], (2.9)
, [мм], (2.9)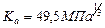 ; для косозубих
; для косозубих  ;
; – допустиме контактне напруження для менш міцного з матеріалів пари зубчастих коліс, МПа;
– допустиме контактне напруження для менш міцного з матеріалів пари зубчастих коліс, МПа;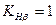 ;
;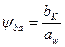 – коефіцієнт ширини вінця колеса, визначають за формулою:
– коефіцієнт ширини вінця колеса, визначають за формулою: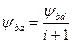 , (2.10)
, (2.10)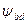 – коефіцієнт ширини колеса по діаметру (табл. 2.6).
– коефіцієнт ширини колеса по діаметру (табл. 2.6).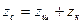 :
: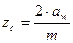 ; (2.11)
; (2.11)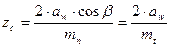 , (2.12)
, (2.12) ;
;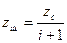 ;
; 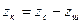 . (2.13)
. (2.13)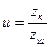 . (2.14)
. (2.14)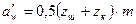 ; (2.15)
; (2.15)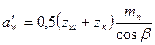 . (2.16)
. (2.16)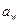 і
і 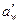 не збігаються, приводять
не збігаються, приводять 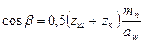 ;
; . (2.17)
. (2.17)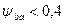 , необхідно перевірити виконання умови:
, необхідно перевірити виконання умови: . (2.18)
. (2.18)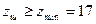 , потім визначити zк і модуль:
, потім визначити zк і модуль: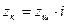 ;
; 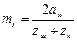 ;
;  . (2.19)
. (2.19) ;
; 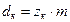 ; (2.20)
; (2.20) ;
; 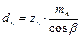 ; (2.21)
; (2.21)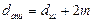 ;
;  ; (2.22)
; (2.22)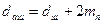 ;
; 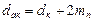 ; (2.23)
; (2.23)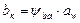 ;
; ;
;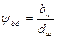 ;
;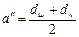 була рівна раніше принятому aw.
була рівна раніше принятому aw.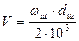 , [м/с], (2.24)
, [м/с], (2.24)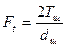 ; (2.25)
; (2.25)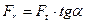 ; (2.26)
; (2.26) ; (2.27)
; (2.27) ; (2.28)
; (2.28) , (2.29)
, (2.29)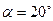 ;
; i порівнюють з допустимими
i порівнюють з допустимими  :
: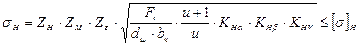 , (2.30)
, (2.30)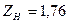 ;
; 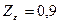 ; для косозубих
; для косозубих  ;
;  ; для стальних коліс
; для стальних коліс 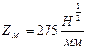 ;
; , для косозубих коліс КНα приймають за табл. 2.9;
, для косозубих коліс КНα приймають за табл. 2.9;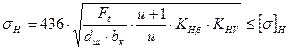 ; (2.31)
; (2.31)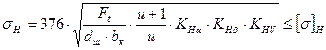 , (2.32)
, (2.32)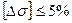 і недовантаження
і недовантаження  . Якщо ці умови не виконуються, змінюють величину bк не виходячи за межі рекомендованих значень Ψbd; якщо це не допомагає, змінюють значення міжосьової відстані aw, вибирають інші матеріали або назначають інший вид термічної обробки і повторюють розрахунки.
. Якщо ці умови не виконуються, змінюють величину bк не виходячи за межі рекомендованих значень Ψbd; якщо це не допомагає, змінюють значення міжосьової відстані aw, вибирають інші матеріали або назначають інший вид термічної обробки і повторюють розрахунки.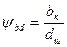
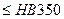
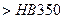
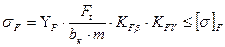 ; (2.33)
; (2.33) , (2.34)
, (2.34) ; (2.35)
; (2.35)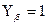 ;
;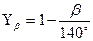 ; (2.36)
; (2.36)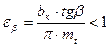 приймають
приймають 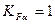 ;
;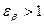 , КFα визначають за формулою:
, КFα визначають за формулою: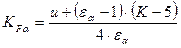 , (2.37)
, (2.37) , (2.38)
, (2.38)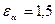 і 8-ю ступенею точності можна приймати
і 8-ю ступенею точності можна приймати  ;
;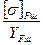 і колеса
і колеса  .
.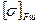 і
і 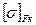 , YFш і YFк допустимі напруження згину і коефіцієнти форми зубів шестірні і коліс.
, YFш і YFк допустимі напруження згину і коефіцієнти форми зубів шестірні і коліс.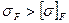 , вибирають інше значення модуля, визначають zш і zк і повторюють перевірочний розрахунок на згин.
, вибирають інше значення модуля, визначають zш і zк і повторюють перевірочний розрахунок на згин. допускається, оскільки навантажувальна здатність закритих передач обмежується контактною міцністю.
допускається, оскільки навантажувальна здатність закритих передач обмежується контактною міцністю.


