Розв’язання. Порядок вибору матеріалів і визначень допустимих напружень для коліс див
Порядок вибору матеріалів і визначень допустимих напружень для коліс див. с. 17…20. З метою скорочення об’єму даного посібника приймаємо для коліс конічної передачі ті ж матеріали і допустимі напруження, що і при розрахунку циліндричної передачі: для шестірні – сталь 45, термообробка – покращення, границя текучості Визначаємо середній ділильний діаметр шестірні за формулою (2.39):
де
і=3,15 – передаточне відношення;
Ширина вінця колеса (формула 2.44):
Визначаємо: – кути ділильних конусів (формула 2.45): колеса шестірні – зовнішній діаметр шестірні:
– зовнішня конусна відстань:
Перевіряємо умову (2.40):
Умова (2.40) виконується. Вибираємо зовнішній модуль
приймаємо Визначаємо: – число зубів шестірні приймаємо – число зубів колеса приймаємо – передаточне число Передаточне число
Уточнюємо: – кути ділильних конусів:
– зовнішній ділильний діаметр шестірні:
– зовнішня конусна відстань:
– середній ділильний діаметр шестірні:
– коефіцієнт ширини вінця колеса по діаметру:
Перевіряємо умову (2.40):
Умова (2.40) виконується. Визначаємо: – зовнішній ділильний діаметр колеса:
– середній ділильний діаметр колеса:
– середній модуль:
– зовнішній діаметр вершин зубів: шестірні:
колеса:
– колову швидкість коліс:
– сили в зачепленні на зубах шестірні: колова:
радіальна:
осьова:
– сили в зачепленні на зубах колеса: колова:
радіальна:
осьова:
За табл. 2.7 назначаємо 8-му степінь точності коліс. За формулою (2.60) проводимо перевірку робочих поверхонь зубів коліс на контактну міцність:
де
Перевантаження складає:
що більше допустимого: Щоб умова (2.60) виконувалась, збільшимо величину ширини вінця колеса Визначаємо:
Перевіряємо умову (2.40):
Визначаємо модуль
округляємо до стандартного (с. 22) і приймаємо Визначаємо: – число зубів шестірні:
приймаємо – число зубів колеса:
приймаємо – передаточне число Відхилення між передаточним відношенням і числом:
відхилення в нормах допустимого Уточнюємо:
Умова (2.40) Визначаємо:
Швидкість:
Сили в зачепленні на зубах шестірні: колова:
радіальна:
осьова:
Сили в зачепленні на зубах колеса:
За табл. 2.7 назначаємо 8-ю степінь точності колеса. Проводимо перевірку робочих поверхонь зубів коліс на контактну міцність:
де
недовантаження складає:
що знаходиться в границях норми, тобто Знаходимо еквівалентне число зубів: шестірні колеса За таблицею 2.11 коефіцієнт форми зуба шестірні
Менш міцними на згин є зуби колеса. Розрахункове напруження зубів колеса на згин визначаємо за формулою (2.63):
де
Умова міцності зубів на згин виконується.
|

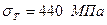 , твердість НВ230, допустиме контактне напруження
, твердість НВ230, допустиме контактне напруження  , напруження згину
, напруження згину  ; для колеса – сталь 45, термообробка – нормалізація, границя текучості
; для колеса – сталь 45, термообробка – нормалізація, границя текучості  , твердість НВ190, допустиме контактне напруження
, твердість НВ190, допустиме контактне напруження  , допустиме напруження згину
, допустиме напруження згину 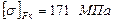 . Граничні допустимі контактні напруження колеса (як менш міцного):
. Граничні допустимі контактні напруження колеса (як менш міцного): 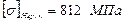 ; згину
; згину 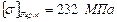 .
. ,
, – момент на валу шестірні:
– момент на валу шестірні: ;
;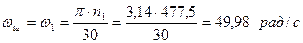 ;
; ;
;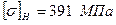 – допустимі контактні напруження; (приймаємо менше значення із отриманих значень допустимих напружень шестірні і колеса);
– допустимі контактні напруження; (приймаємо менше значення із отриманих значень допустимих напружень шестірні і колеса);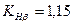 – коефіцієнт нерівномірності навантаження по довжині зуба (табл. 2.10);
– коефіцієнт нерівномірності навантаження по довжині зуба (табл. 2.10); – коефіцієнт ширини вінця по діаметру (табл. 2.6);
– коефіцієнт ширини вінця по діаметру (табл. 2.6);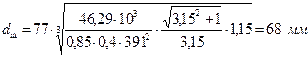 .
. .
. ;
; ;
; ;
;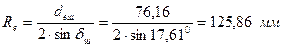 .
.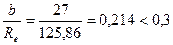 .
. з урахуванням умови (2.40):
з урахуванням умови (2.40):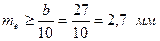 ,
, згідно стандарту (с. 22).
згідно стандарту (с. 22). ,
, ;
;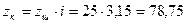 ,
,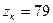 ;
;
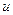 відрізняється від передаточного відношення і на:
відрізняється від передаточного відношення і на: .
.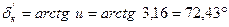 ;
;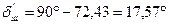 ;
;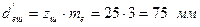 ;
; ;
;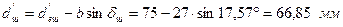 ;
; .
. .
. ;
; ;
; ;
;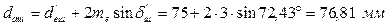 ;
;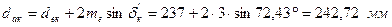 ;
; ;
; ;
; ;
;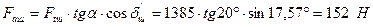 ;
; ;
;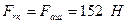 ;
;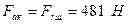 .
. ,
, – колова сила;
– колова сила;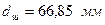 – середній діаметр шестірні;
– середній діаметр шестірні; – ширина вінця шестірні;
– ширина вінця шестірні; і консольному розташуванні коліс;
і консольному розташуванні коліс;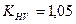 – коефіцієнт динамічності, (табл. 2.8 при швидкості до 5 м/с і 8-й степені точності коліс);
– коефіцієнт динамічності, (табл. 2.8 при швидкості до 5 м/с і 8-й степені точності коліс); – передаточне число;
– передаточне число; ;
; .
. ,
, .
. . За таблицею 2.6 приймаємо
. За таблицею 2.6 приймаємо 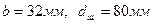 і повторюємо розрахунок.
і повторюємо розрахунок.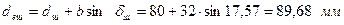 ;
;
 .
. ,
,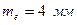 .
. ,
, ;
;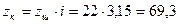 ,
, ;
;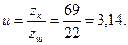
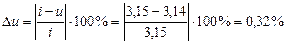 ,
, .
. ;
;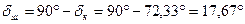 ;
;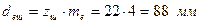 ;
;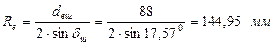 ;
; ;
; .
. виконується.
виконується. ;
;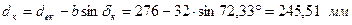 ;
; ;
; ;
;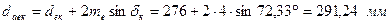 .
. .
.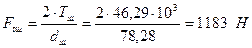 ;
;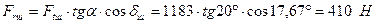 ,
, .
. ,
,  ,
,  .
. ,
, ;
;  ;
;  ;
;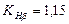 (за табл. 2.10 при
(за табл. 2.10 при 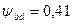 );
); (табл. 2.8);
(табл. 2.8);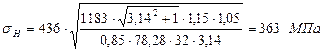 .
. ,
,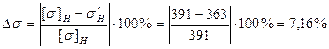 ,
, .
. ;
;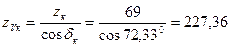 .
. (при
(при 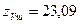 ), і колеса
), і колеса 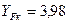 (при
(при  ). Проводимо порівняльну оцінку міцності зубів шестірні і колеса на згин:
). Проводимо порівняльну оцінку міцності зубів шестірні і колеса на згин: ;
; .
.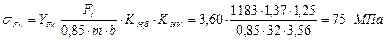 ,
,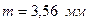 – середній модуль;
– середній модуль; 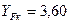 – коефіцієнт форми зуба;
– коефіцієнт форми зуба; 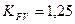 – коефіцієнт нерівномірності навантаження по довжині зуба (табл. 2.13).
– коефіцієнт нерівномірності навантаження по довжині зуба (табл. 2.13). .
.


