Лабораторная работа N1
АЛГОРИТМ СЕКУЩИХ ПЛОСКОСТЕЙ
Цель: изучение алгоритма секущих плоскостей, разработка на его основе обучающейся системы распознавания изображений.
Краткие сведения Алгоритм обучения машины «узнаванию» образов, основанный на методе секущих гиперплоскостей, заключается в аппроксимации разделяющей гиперповерхности «кусками» гиперплоскостей и состоит из следующих частей: А. Обучение (формирование разделяющей поверхности) *): (1) проведение секущих плоскостей; (2) исключение лишних плоскостей; (3) исключение лишних кусков плоскостей. Б. Распознавание новых объектов. § 1. Геометрическая иллюстрация алгоритма
Вначале проследим построение алгоритма на условных геометрических иллюстрациях. Предположим, что нам предстоит обучить машину распознаванию трех образов**),которые мы условимся называть образами А, В и С. В пространстве рецепторов этим образам соответствуют три нам неизвестных, но объективно существующих компактных множества точек. На рис. 1 эти множества изображены в виде трех областей А, В и. С.
Рис.1. Образы А,В и С
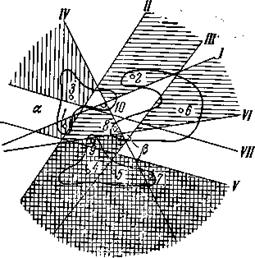
Проведение секущих плоскостей. В машину вводятся коды двух точек, принадлежащих разным образам. Машина запоминает координаты точек в пространстве рецепторов (точки 1 и 2 на рис. 2) и проводит произвольную плоскость I, разделяющую эти точки. Пространство рецепторов оказывается разбитым на два полупространства, каждое из которых на данном этапе алгоритма отождествляется с одним из двух образов.
Разбиение может оказаться очень неудачным, как это и есть на рис. 2, где большая часть области В лежит, в результате проведенной нами процедуры, в полупространстве, отнесенном к образу А. После проведения первой плоскости в машину вводится третий объект. Возможны два случая: 1) объект относится к образам А или В и попадает в полупространство, отнесенное к «своему» образу. При этом машина, запомнив координаты появившегося объекта, готова к восприятию следующего; 2) объект либо относитсяк образу С, либо, являясь объектом образов А или В, попадает не в«свое» полупространство. Тогда в одном полупространстве оказываются точки, относящиеся к разным образам. Назовем такой случай противоречием. В нашем случае точка 3 (рис.2), относящаяся к образу А, попадает в полупространство, отнесенное ранее к образу В, и вступает в противоречие с точкой 2. (Точки, с которыми очередной объект вступает в противоречие, будем называть оппонентами). Машина ликвидирует противоречие, проводя плоскость //, разделяющую оппонент (точку 2) и точку 3. Теперь машина относит к образу А области abc и abd, а к образу В— область аЬе (рис. 3).
// Рис.3. Проведение II секущей плоскости
После проведения второй плоскости число частей, на которое разбивается пространство рецепторов, оказывается больше числа появившихся точек. При проведении последующих плоскостей число частей пространства возрастает чрезвычайно быстро (приблизительно как 2n, где п — количество плоскостей), значительно быстрее, чем число точек. Поэтому проведение новых плоскостей, уточняя границы областей А, В, С, одновременно сопровождается появлением большого числа «пустых» частей пространства, которые не могут быть отнесены к какому-либо образу (например, область сbе на рис. 3). Появление новой точки теперь может привести к трем ситуациям: 1) возникает противоречие; 2) противоречие не возникает, так как точка попадает в «свою» часть пространства; 3) противоречие не возникает, так как точка попадает в «пустую», не поименованную часть пространства. В этом случае машина запоминает координаты новой точки и относит область, в которую попала эта точка, к соответствующему образу. Именно такая ситуация возникает при появлении точки 4 (рис. 4).
Рис.4. Построение 4,5 и 6 точек
Не возникает противоречия и при появлении точки 5. Машина запоминает координаты точек 4 и 5, но не проводит новых плоскостей, относя всю область cbe к образу С. Появление шестой точки приводит к противоречию, причем у точки 6 оказывается сразу два оппонента — точки 4 и 5. Вначале проводится плоскость ///, разделяющая точки 6 и 4, затем плоскость /V, разделяющая точки 6 и 5 (рис. 5).
Рис.5. Проведение /// и /V секущих плоскостей
Точка 7 (рис. 5) вступает в противоречие с точкой 6, что приводит к появлению плоскости V (рис. 6). Рис.6. Проведение V секущей плоскости
Точка 8 попадает в «пустую» часть пространства, но затем становится оппонентом точки 9 (рис. 7).. Рис.7. Построение 8 и 9 точек
Рис.8. Проведение VI и VII секущих плоскостей
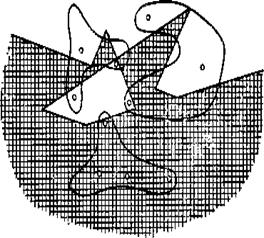
Следует обратить внимание на то, что с увеличением числа введенных в машину объектов и количества секущих плоскостей противоречия будут возникать между объектами и оппонентами, лежащими все ближе и ближе к границам областей А, В, С. Область пространства, в которой возможны противоречия, все время сужается, и вероятность возникнования противоречия при появлении нового объекта становится все меньше и меньше, так как убывает число неправильно поименованных областей. Частота возникновения противоречий может, таким образом, служить критерием завершения первой части алгоритма. Закончим первую часть алгоритма проведением плоскости VII. Сложившаяся ситуация приведена на рис. 9. Рис. 9. Разбиение пространства на ряд областей
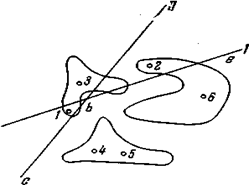
Пространство разбито на ряд областей. Некоторые из них содержат хотя бы одну точку и отнесены машиной к соответствующим образам. Эти области отмечены на рис. 9 различной штриховкой. Остальные области (их горазо больше, чем первых) остались «пустыми» и ни к какому образу не отнесены. Совершенно ясно, что на этом нельзя заканчивать процесс обучения. Подлежащая определению новая точка может попасть в «пустую» область и ее нельзя будет отнести ни к какому образу. Необходимо каким-то способом поименовать все без исключения области пространства. Продолжение первой части алгоритма, разумеется, не может привести к этой цели, так как число «пустых» областей будет все быстрее и быстрее опережать число появившихся точек. Обратимся к основной нашей идее — предположению о компактности множеств точек, соответствующих образам. Исходя из этого предположения, естественно отнести «пустые» области к тем же образам, что и какая-нибудь из соседних поименованных областей. При этом такая манипуляция с «пустыми» областями, окруженными одноименными частями пространства, будет совершенно однозначна и не приведет к ошибкам (например, пустая область a на рис. 9 вполне определенно относится к образу А). Только при операциях с областями, лежащими у границ множеств, будут возможны неоднозначность и ошибки. «Пустая» область b (см. рис. 9), например, может быть ошибочно отнесена к образу С. Расширение поименованных частей пространства можо представить как выбрасывание кусков плоскостей, отделяющих «пустые» области от соседних поименованных. Разумеется, как лишние, могут выбрасываться также и куски плоскостей, разделяющие одноименные области. Оставшиеся после такой операции куски плоскостей и обазуют искомую разделяющую гиперповерхность. Весьма важно выбрасывать куски плоскостей более или менее равномерно по пространству. Не соблюдая этого правила, можно прийти к заведомо неправильной разделяющей поверхности. Если например, начав с некоторой поименованной области, присоединить к ней все соседние «пустые», к образовавшейся области — все «пустые», соседние с ней и т. д., можно почти все пространство отнести к тому же образу, что и исходная область, ибо после окончания первой части алгоритма поименованные области, как редкие островки, «затеряны» среди областей не поименованных. На рис. 10 заштрихована область, которую можно отнести к образу С, если действовать таким методом, начиная с одной из поименованных облатей этого образа.
Рис. 10. Область, отнесенная к образу С
Для того чтобы обеспечить более или менее равномерное выбрасывание кусков плоскостей, можно прибегнуть к следующему приему. Вначале следует выяснить, нет ли плоскостей, которые целиком состоят из лишних кусков, и, если такие найдутся, выбросить эти плоскости. Затем сначала выбросить «лишние» куски одной из оставшихся плоскостей, потом другой и т.д. Можно доказать, что при этом поименованными окажутся все части пространства.
|


 Рис.2. Проведение I секущей плоскости
Рис.2. Проведение I секущей плоскости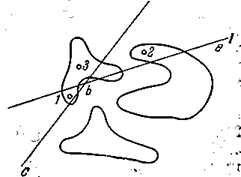

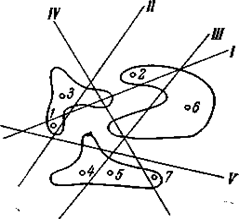
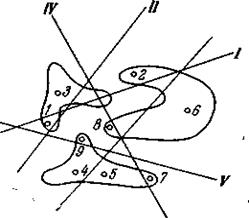
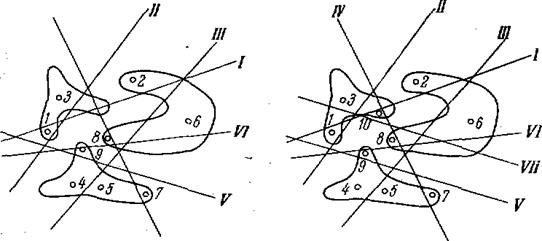 Противоречие ликвидируется плоскостью VI (рис. 8). Появление десятой точки, вступающей в противоречие с точкой 8, приводит к появлению плоскости VII (рис. 8).
Противоречие ликвидируется плоскостью VI (рис. 8). Появление десятой точки, вступающей в противоречие с точкой 8, приводит к появлению плоскости VII (рис. 8).