Распознавание новых объектов.
При предъявлении нового объекта машина вычисляет его знаки относительно всех плоскостей и полученный код поочередно сравнивает по существенным разрядам со всеми строками таблицы знаков (табл. X). При совпадении строк машина относит новый объект к соответствующему образу.
§ 3. Способы повышения надежности распознавания Секущие плоскости проводятся случайно и независимо друг от друга. Поэтому, если провести обучение несколько раз на одном и том же материале (т. е. осуществить несколько вариантов обучения), будет весьма маловероятным, что ошибки в разбиении пространства рецепторов окажутся одинаковыми во всех вариантах. Следует ожидать, что в каждом из вариантов машина будет ошибаться по-разному. Это дает основание применить метод параллельных вариантов. При использовании этого метода одновременно и независимо друг от друга на одном и том же материале обучаются несколько машин. При узнавании новых объектов каждая машина будет относить эти объекты к какому-то образу, может быть, не к одному и тому же. Окончательное решение принимается «голосованием» машин — объект относится к тому образу, к которому его отнесло большее число машин. Эксперименты показывают, что метод параллельных вариантов весьма эффективен. Другой способ повышения надежности распознавания состоит в некотором улучшении метода проведения секущих плоскостей. Можно предположить, что если проводить секущие плоскости близко к плоскости, проходящей через середину прямой, соединяющей объект и оппонент и перпендикулярной к этой прямой[1], то результирующая разделяющая поверхность будет ближе к истинной границе между образами. Эксперименты подтверждают это предположение. В экспериментах с «улучшенным» алгоритмом проведение секущих плоскостей происходило следующим образом. Выбиралось некоторое число k (его величина уточнялась экспериментом), и после случайного выбора величин li, и вычисления s(1) и s(2) (см. первую часть алгоритма) модуль разности s(1) и s(2) сравнивался с k. Если |s(1) - s(2)| > k, выбранные li считались пригодными и вводились в память машины; если |s(1) - s(2)| £ k, то li выбирались вновь до тех пор, пока модуль разности s(1) и s(2) не превзойдет k. Кроме того, в качестве свободного члена выбиралось число
Геометрически эти условия означают, что секущая плоскость SS проходит через середину прямой, соединяющей объект и оппонент, и располагается внутри некоторого угла АОВ вблизи перпендикуляра ОС к этой прямой (рис. 13), причем этот угол тем меньше, чем больше величина k.
Метод параллельных вариантов позволяет еще больше повысить надежность распознавания. Применение этого метода к вариантам первоначального алгоритма позволило машине правильно узнать 88,5% фигур, а когда метод был применен к вариантам улучшенного алгоритма, надежность узнавания возросла до 98,5%, т. е. машина ошибалась только в трех случаях из двухсот. Таким образом, эксперименты показали, что метод секущих плоскостей действительно позволяет обучить машину распознаванию сложных фигур. А так как никакие сведения о свойствах фигур машине не сообщались, этот же алгоритм в принципе дает машине возможность обучиться распознаванию широкого класса иных образов, аналогичных по сложности арабским цифрам.
|

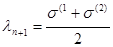
 (6)
(6) В экспериментах с «улучшенным» алгоритмом при k = 2 и при k = 5 средний процент правильно узнанных фигур повысился почти до 80% при k =2 и более чем до 85% при k = 5. Один из вариантов при k = 5 дал надежность распознавания почти 90 %. Такое резкое повышение надежности распознавания за счет более организованного проведения секущих плоскостей говорит о том, что гипотеза компактности справедлива, по крайней мере, в отношении применявшихся образов. В противном случае разные методы проведения плоскостей давали бы примерно одинаковый эффект.
В экспериментах с «улучшенным» алгоритмом при k = 2 и при k = 5 средний процент правильно узнанных фигур повысился почти до 80% при k =2 и более чем до 85% при k = 5. Один из вариантов при k = 5 дал надежность распознавания почти 90 %. Такое резкое повышение надежности распознавания за счет более организованного проведения секущих плоскостей говорит о том, что гипотеза компактности справедлива, по крайней мере, в отношении применявшихся образов. В противном случае разные методы проведения плоскостей давали бы примерно одинаковый эффект.


