Multiple Regression Analysis. Derivation of the Multiple Regression Coefficients.
Derivation of OLS estimators As in the simple regression case, we choose the values of the regression coefficient to make the fit as goog as possible in the hope that we will obtaine the most satisfactory estimates of the unknown true parameters. Our definition of goodness of fit is the minimization of RSS, the sum of squares of the residuals: RSS=
where b1, b2.... bk are estimates of the true regression coefficients b1, b2,.......bk, given a sample of n observations on Y and all the X’s; ei = Yi -
The OLS estimators are obtained by minimising the residual sum of squares (RSS): RSS = The k first order conditions for this problem are known as the normal equations for the regression coefficients:
¶ RSS /¶ b1 = ¶ RSS /¶ b2 = ¶ RSS /¶ b3 = M M ¶ RSS /¶ bk = We can derive the OLS estimator for b1 from (1) as: b1 = where b1 is the predicted value of Y when the values of all the explanatory variables are set equal to zero. We can the proceed to derive estimators for the k -1 unknown slope coefficients b2, b3,...bk from the remaining k -1 simultaneous equations. These estimators are complicated expressions in which each bj depends in general on the sample values of the dependent variable and all of the explanatory variables. Slope estimators when k -1 = 2 You well never need to know the formulae for the slope estimators for use in practical work since the computer will perform all the necessary calculations. Nevertheless some insights into the general nature of the slope estimators in multiple regression can be obtained by examining the estimators for the particular case where there are two explanatory variables (i.e. k -1 =2). Thus when k -1 =2 we obtain: The estimator b2 depends not only on the observed values of X2 and Y but also on those of X3. Thus the slope coefficient on X2 will not generally be the same as that obtained from a simple regression of Y on a constant and X2. Moreover we can not generally obtain the full set of regression coefficients by performing two simple regressions, one of Y on a constant and X2 and the other of Y on a constant and X3, and somehow combining the results. First, the principles behind the derivation of the regression coefficient are the same for multiple regression as for simple regression. Second, the expression, however, are different and so you should not try to use expressions derived for simple regression in a multiple regression context. 33.Properties of the Multiple Regression Coefficients: unbiasedness, efficiency, precision, consistency. PROPERTIES OF THE OLS REGRESSION COEFFICIENTS MODEL SPECIFICATION Define the true regression model as: yi = b + Xi + ui Where yiis composed of (i) a systematic portion b + Xi whose specification is guided by economic theory and (ii) a random component given by the disturbance term ui Given the Gauss-Markov condition E{ ui } = 0 then E{ yi } = b + Xi Define the estimated regression line as:
where b and b are the OLS estimates of the true regression coefficients and given a sample of n observations on X and Y:
b= b Linearity of the OLS estimators. We can note that both b and b are linear estimators since they can be written as linear functions of the Yi ’s (i.e. in the form S wiYi where the weights, wi, depend on the (fixed) values taken by the explanatory variable) EXPECTED VALUES OF THE OLS ESTIMATORS Each regression coefficient can be decomposed or broken down into (i) a fixed component equal to the value of the true regression parameter (ii) a random component dependent on u which is responsible for its variations around the central tendency: b We can then show that: E{b} = if Gauss-Markov conditions 1 and 4 hold E{b} = if Gauss-Markov condition 4 holds Unbiasedness of the OLS estimators. An estimator is said to be unbiased if the expected value of the estimator is equal to the population characteristic. Sample estimates derived from an unbiased estimator will be accurate on average, though individual estimates (obtained from particular samples) will only equal the true value by coincidence. precision of the ols estimators The population variances of the OLS estimators are: pop.var{b} where The population variance of the disturbance term will in general be unknown. An unbiased estimator of
where ei= Yi (b + bXi) are the residuals from the estimated regression, and nk is the number of degrees of freedom (n is the sample size and k is the number of coefficients in the regression (which is equal to 2 in the simple bivariate model)). The square root of this estimator su is known as the (sample) Standard Error of the Regression (S.E.R) and provides an estimator of the typical size of the disturbance term in the regression model. Estimators for the standard errors of b and b are therefore given as: s.e.{b} s.e.{b} The standard error of a regression coefficient is a measure of the typical deviation of a sample estimate of the coefficient from the true parameter value (i.e. of the typical size of the estimation error). Efficiency of the OLS estimators. One unbiased estimator is said to be more efficient than another if it has the smaller variance of the two estimators. The more efficient an estimator is the more likely it is that an estimate obtained using the estimator from a particular sample will be close to the value of the population characteristic. The minimum variance unbiased estimator has the smallest variance of any possible unbiased estimator (of its type). Consistency of the OLS estimators An estimator is said to be consistent if the probability limit (plim) of the estimator is equal to the true value of the population characteristic. A consistent estimator is bound to give an accurate estimate if the sample size is large enough, regardless of the actual observations in the sample.
|

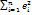 , where ei is the residual in observation I, the difference between the actual value Yi in that observation and the value
, where ei is the residual in observation I, the difference between the actual value Yi in that observation and the value 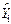 predicted by the regression equation:
predicted by the regression equation: = b1 + b2X2i + b3X3i +........ + bkXki;
= b1 + b2X2i + b3X3i +........ + bkXki; defines the predicted or estimated value of Yi given the values X2i, X3i,.......Xki, and
defines the predicted or estimated value of Yi given the values X2i, X3i,.......Xki, and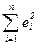 =
= 
 = 0 (1)
= 0 (1)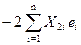 = 0 (2)
= 0 (2) = 0 (3)
= 0 (3)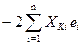 = 0 (k)
= 0 (k)
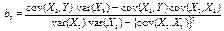 and a parallel expression for b3 can be obtained by exchanging X2 and X3.
and a parallel expression for b3 can be obtained by exchanging X2 and X3.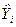 = b + bXi
= b + bXi b
b  =
= 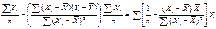

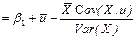 ; b
; b 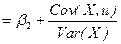
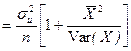 ; pop.var{b}
; pop.var{b} 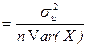 ;
; = E[
= E[ 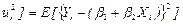 is the population variance of the disturbance term. Both pop.var{b} and pop.var{b} are (i) directly proportional to
is the population variance of the disturbance term. Both pop.var{b} and pop.var{b} are (i) directly proportional to 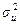 is given by:
is given by:

 ;
;


