Ряды Фурье.
Определение. Рядом Фурье функции f(x), определённой и интегрируемой на отрезке
коэффициенты которого определяются формулами
Если ряд (1) является рядом Фурье функции f(x), то пишут
Если f(x)= f(-x),т.е. f(x) – функция чётная, то
Если f(x)=- f(x),т.е. f(x) – функция нечётная, то Пример. Разложить в ряд Фурье функцию На рисунке (рис.1) изображён график заданной функции.
Условиям теоремы функция Ряд Фурье содержит только синусы:
При этом
Гармоническое колебание (движение) описывается функцией
где Основным периодом функции (3) является Ряд Фурье с периодом 2 l. Теорема. Если функция f(x) и её производная
где
а в каждой точке Если функция f(x) с периодом
|

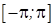 , называется ряд
, называется ряд (1)
(1)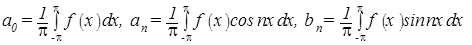 .
.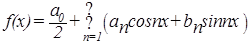 . (2)
. (2)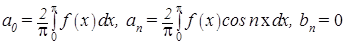 и
и 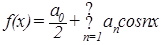 .
.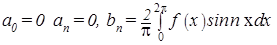 и
и 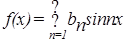 .
.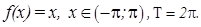
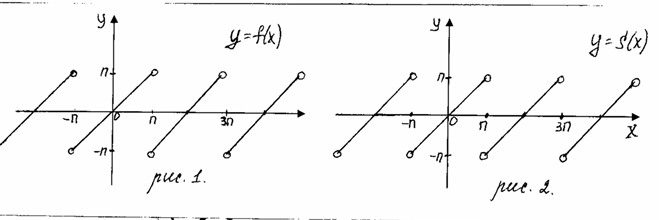
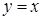 удовлетворяет. Эта функция – нечётная. Следовательно,
удовлетворяет. Эта функция – нечётная. Следовательно, 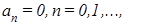 а
а 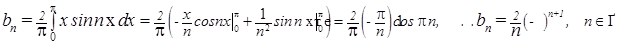 .
.
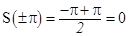 (рис.2).
(рис.2).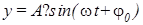 , (3)
, (3) - амплитуда колебания,
- амплитуда колебания, 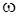 - частота,
- частота, 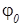 - начальная фаза,
- начальная фаза, 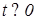 .
. , т.е. одно полное колебание совершается за промежуток времени
, т.е. одно полное колебание совершается за промежуток времени 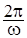 (
(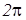 единиц времени).
единиц времени).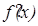 – непрерывны на отрезке
– непрерывны на отрезке 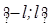 (l>0) или же имеют на нём конечное число точек разрыва I-го рода, то во всех точках
(l>0) или же имеют на нём конечное число точек разрыва I-го рода, то во всех точках 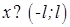 , в которых f(x) непрерывна, сумма ряда равна f(x) и справедливо разложение
, в которых f(x) непрерывна, сумма ряда равна f(x) и справедливо разложение (4)
(4)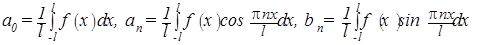 ,
, разрыва функции сумма ряда равна
разрыва функции сумма ряда равна 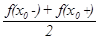 и на концах отрезка сумма ряда равна
и на концах отрезка сумма ряда равна  .
. удовлетворяет условиям теоремы, то для неё имеет место разложение (1), где коэффициенты вычисляются по формулам
удовлетворяет условиям теоремы, то для неё имеет место разложение (1), где коэффициенты вычисляются по формулам 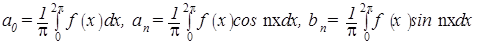 .
.


