Игра – упрощенная математическая модель конфликтной ситуации, отличающаяся от реального конфликта тем, что ведется по определенным правилом.  – платежная матрица.
– платежная матрица.  – элемент матрицы, i – номер строки, j – номер столбца. Нижняя цена игры: М1=
– элемент матрицы, i – номер строки, j – номер столбца. Нижняя цена игры: М1= 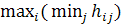 . Верхняя цена игры: М2=
. Верхняя цена игры: М2=  .
.
Для матричной игры справедливо неравенство 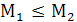 . Если
. Если 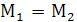 =
=  – седловая точка матрицы – элемент матрицы – цена игры.
– седловая точка матрицы – элемент матрицы – цена игры.
Пример. Имеется платежная матрица 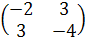 . Определим верхнюю и нижнюю цену игры. Нижняя цена игры: М1=
. Определим верхнюю и нижнюю цену игры. Нижняя цена игры: М1=  Верхняя цена игры: М2=
Верхняя цена игры: М2= 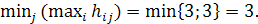
Пример. Матрица выигрышей с природой имеет вид
|
| P(Q1)=0,2
| P(Q2)=…
|
| А1
|
|
|
| А2
|
|
|
| А3
|
|
|
| А4
|
|
|
Определим стратегию с помощью которой достигается наибольший средний выигрыш. Значение P(Q2)=1–P(Q1)=1–0,2=0,8. Найдем Средний выигрыш для каждой стратегии: 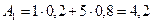 ,
, 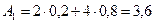 ,
, 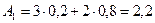 ,
, 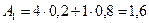 . Таким образом, стратегия А1.
. Таким образом, стратегия А1.

 – платежная матрица.
– платежная матрица.  – элемент матрицы, i – номер строки, j – номер столбца. Нижняя цена игры: М1=
– элемент матрицы, i – номер строки, j – номер столбца. Нижняя цена игры: М1= 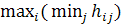 . Верхняя цена игры: М2=
. Верхняя цена игры: М2=  .
.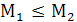 . Если
. Если 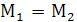 =
=  – седловая точка матрицы – элемент матрицы – цена игры.
– седловая точка матрицы – элемент матрицы – цена игры.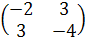 . Определим верхнюю и нижнюю цену игры. Нижняя цена игры: М1=
. Определим верхнюю и нижнюю цену игры. Нижняя цена игры: М1=  Верхняя цена игры: М2=
Верхняя цена игры: М2= 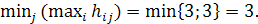
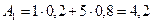 ,
, 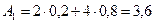 ,
, 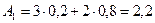 ,
, 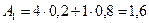 . Таким образом, стратегия А1.
. Таким образом, стратегия А1.


