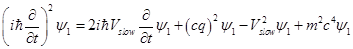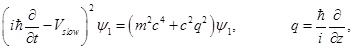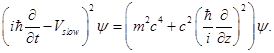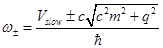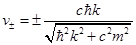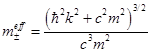Supplementary Material
The Hamiltonian which describes the Dynamics of atoms in the bichromatic lattice is:
The eigenvalue equation for this Hamiltonian will be
where
Here
Equating the coefficients of each
or eigenvalue equation
where
and
Now let`s find the eigenvalues of this matrix.
We are especially interested for the eigenvalues in the second and third Bloch band for a quasi-momentum
Since the Bloch bands are in the vicinity of
In the next step, the difference between the two eigenvalues is then calculated to obtain information about the energy split between the second and third Bloch-Bands.
(When
From Eq. (1.12)
Here the term
From the second equation of the (1.9) system
Adiabatic elimination of the ground state (
thus,
Recalling that
Applying a rotation to Eq.(1.21) with a unitary (
and replacing q by the corresponding operator finally gives an effective Hamiltonian
Where
Consequently,
For a derivation of the full effectively relativistic wave equation Hamiltonian
For each spinor the time-dependent waveequation will be
Taking time-derivative from (1.4) and replacing in it expression for
Next, we find an expression for
Here we multiply both sides by
So,
or,
Dispersion relation can be obtained with the help of plane wave solution
The corresponding group velocities will be
and effective masses:
|

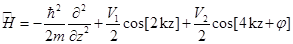
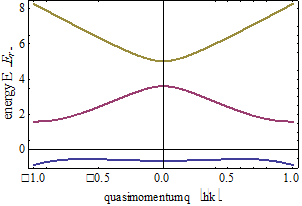 Figure 1 shoes the band structure of such a Fourier-synthesized lattice for
Figure 1 shoes the band structure of such a Fourier-synthesized lattice for 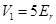 and
and 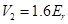 , where
, where 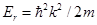 .
.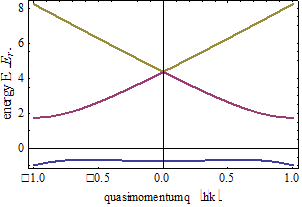 (Сам построил)
(Сам построил)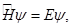
 is the Bloch wavefunction and could be written in the form
is the Bloch wavefunction and could be written in the form
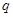 is the quasimomentum that is conventionally restricted to the reduced Brillouin zone
is the quasimomentum that is conventionally restricted to the reduced Brillouin zone  Inserting the wavefunction intoSchrodinger equation we get
Inserting the wavefunction intoSchrodinger equation we get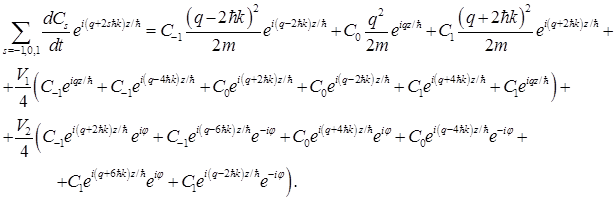
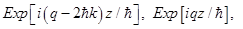 and
and 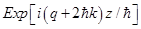 harmonics, we get a system of three differential equations:
harmonics, we get a system of three differential equations: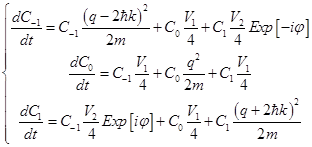
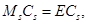
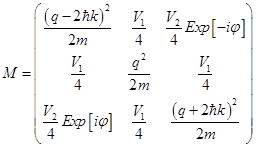 ,
,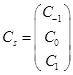
 Taking into account that
Taking into account that 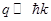 (we work in the center of the Brillouin zone) for M we get
(we work in the center of the Brillouin zone) for M we get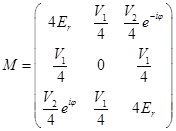
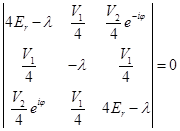
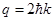 . This should be in the range of
. This should be in the range of 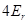 , so that it is useful to introduce a new variable
, so that it is useful to introduce a new variable 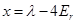 . The determinant will give the following equation for coefficients:
. The determinant will give the following equation for coefficients: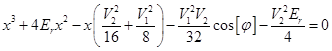
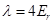 (the crossing point on the Figure1. Is near
(the crossing point on the Figure1. Is near 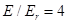 ), the term
), the term  could be neglected, so that the resulting quadratic equation by the coefficient
could be neglected, so that the resulting quadratic equation by the coefficient 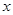 can be resolved
can be resolved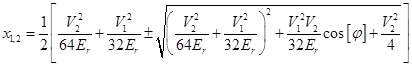
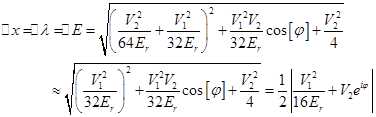
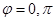
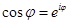 ). Thus,
). Thus,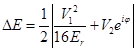
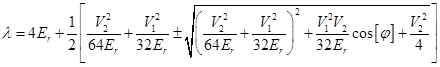
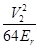 could be neglected, since
could be neglected, since 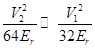 . The last term is the
. The last term is the 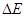 energy difference between the 2nd and 3rd bands, which is
energy difference between the 2nd and 3rd bands, which is 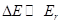 . So, the eigenvalue will be:
. So, the eigenvalue will be: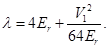
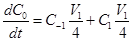
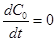 ) leads to
) leads to 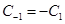 . At the same time
. At the same time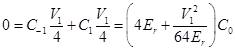
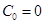 . Refering back to Shrodinger equations for
. Refering back to Shrodinger equations for 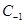 and
and 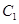 we write
we write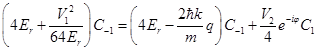


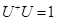 ) transformation matrix
) transformation matrix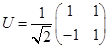
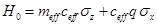
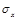 and
and 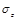 are Pauli matrixes:
are Pauli matrixes: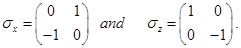
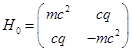
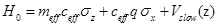 with an external potential
with an external potential 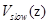 which acts on spinors
which acts on spinors 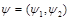 with
with 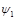 and
and 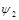 corresponding to course grain atomic wavefunctions in the upper and lower bands, respectively. The corresponding time-dependent wave-equation will be
corresponding to course grain atomic wavefunctions in the upper and lower bands, respectively. The corresponding time-dependent wave-equation will be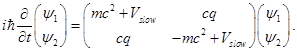

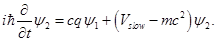
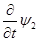 from (1.5) one can get
from (1.5) one can get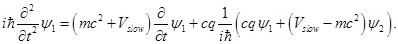
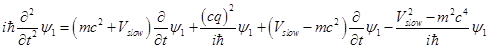
 :
: