ТЕПЛОВОЙ РАСЧЕТ РЕКУПЕРАТИВНОГО ТЕПЛООБМЕННИКА
Различают проектировочный и проверочный тепловой расчет теплообменного аппарата. Цель проектировочного расчета состоит в определении площади рабочей поверхности теплообменника, которая является исходным параметром при его проектировании. При этом должно быть известно передаваемое количество теплоты или массовые расходы теплоносителей и изменение их температуры. Проверочный расчет выполняется для теплообменника с известной площадью поверхности. Цель расчета состоит в определении температур теплоносителя на выходе из теплообменника и передаваемого количества теплоты.
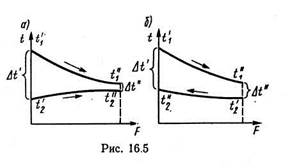
На рис.16.5 изображены температурные поля прямоточного (рис.16.5, а) и противоточного (рис.16.5, б) теплообменников. Индексами «1» и «2» отмечены температуры и другие параметры горячего и холодного теплоносителя соответственно. Одним и двумя штрихами отмечены параметры теплоносителя на входе и выходе из теплообменного аппарата. Сравнение температурных полей прямоточного и противоточного теплообменников показывает, что при противоточной схеме имеется большая возможность изменения температуры теплоносителей в пределах аппарата. Если, например, необходимо нагреть холодный теплоноситель до максимально возможной температуры при заданной начальной температуре горячего теплоносителя Рабочий процесс рекуперативного теплообменника на стационарном режиме работы описывается двумя уравнениями: уравнением теплового баланса и уравнением теплопередачи. Тепловой баланс теплообменника определяется уравнением
где G — массовый расход теплоносителя; Полная теплоемкость массового расхода
С учетом этого обозначения уравнению теплового баланса можно придать вид
Обозначив изменение температуры теплоносителя в пределах теплообменного аппарата через
Следовательно, чем больше параметр W, тем меньше изменяется температура теплоносителя в пределах теплообменного аппарата. Рассмотрим теперь уравнение теплопередачи. Разность температур между теплоносителями изменяется по длине теплообменного аппарата, поэтому уравнение теплопередачи имеет вид
где k и Уравнения теплового баланса и теплопередачи служат основой проектировочного и проверочного расчетов теплообменника. При проектировочном расчете площадь рабочей поверхности теплообменника определяется из уравнения теплопередачи
Если тепловой поток
Получим формулу для подсчета среднего температурного напора. Запишем уравнения теплопередачи и теплового баланса для элемента рабочей поверхности прямоточного теплообменника (рис.16.6):
Из последнего уравнения следует, что
После замены в этом равенстве
После интегрирования этого уравнения от входного до выходного сечения теплообменника получим
С помощью уравнения (16.3) при
Подставив это выражение в формулу (16.8) и заменив в нем величину kF из уравнения (16.5), получим окончательную формулу для определения среднего температурного напора:
Это выражение называется формулой среднелогарифмического температурного напора. Она одинаково пригодна для прямоточного и противоточного теплообменников (величины Аналитическая оценка среднего температурного напора для теплообменников с перекрестным током и другими более сложными схемами движения приводит к громоздким формулам. Поэтому средний температурный напор для таких схем движения теплоносителей определяют по формуле
где Зависимости Полученные формулы позволяют сравнить средние температурные напоры при различных схемах движения теплоносителей. Сравнение показывает, что при одинаковых температурах теплоносителей на входе и выходе из теплообменного аппарата в противоточном теплообменнике температурный напор получается наибольшим, а в прямоточном — наименьшим. При других схемах движения теплоносителя Благодаря большому значению среднего температурного напора площадь рабочей поверхности в противоточной схеме при прочих равных условиях будет наименьшей. Поэтому, если причины конструктивного характера не ограничивают выбор схемы движения теплоносителей, то предпочтение надо отдать противоточному теплообменнику по сравнению с прямоточным. Но следует заметить, что противоточная схема движения теплоносителей не всегда имеет существенные преимущества перед прямоточной. Расчеты показывают, что при большом значении одного из параметров W( При сравнении противоточной и перекрестной схем движения необходимо принять во внимание не только изменение среднего температурного напора, но и изменение условий теплообмена. При одинаковом гидравлическом сопротивлении и условии Если величины
При Для подсчета площади рабочей поверхности по выражению (16.5) коэффициент теплопередачи определяется обычно по формулам плоской стенки, так как трубки теплообменника имеют небольшую толщину. Если в пределах аппарата условия теплообмена на отдельных участках рабочей поверхности существенно различны, то коэффициенты теплообмена и теплопередачи подсчитываются для каждого участка отдельно, а затем определяется для всей поверхности значение коэффициента теплопередачи по формуле где Средние температуры теплоносителей, необходимые для расчета коэффициентов теплообмена, определяются следующим образом. Для теплоносителя с большой величиной параметра W, у которого температура в пределах теплообменника изменяется меньше, средняя температура определяется как полусумма крайних значений температур. Если
Средняя температура второго теплоносителя определяется по формуле
где Получим расчетные соотношения для выполнения проверочного расчета прямоточного теплообменника. Если обозначить
то уравнение (16.8) можно переписать в виде
Вычтем из единицы правую и левую части равенства:
После приведения к общему знаменателю и перегруппировки членов левой части равенства имеем
Из уравнения теплового баланса при
Подставив это равенство в выражение (16.13), после несложных преобразований получим
где
Для конечной температуры холодного теплоносителя в прямоточном теплообменнике расчетная формула имеет вид
Аналогично для противоточного теплообменника:
где
Для определения функций После определения конечных температур тепловой поток подсчитывается по уравнению (16.3).
|

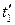 , то при увеличении поверхности нагрева в прямоточном теплообменнике температура
, то при увеличении поверхности нагрева в прямоточном теплообменнике температура 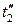 будет приближаться к температуре
будет приближаться к температуре  , а в противоточном — к
, а в противоточном — к 
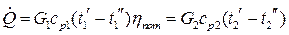 , (16.1)
, (16.1)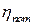 — коэффициент потерь теплоты в окружающую среду, который равен 0,97...0,995;
— коэффициент потерь теплоты в окружающую среду, который равен 0,97...0,995;  и
и 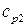 — средние удельные теплоемкости теплоносителей.
— средние удельные теплоемкости теплоносителей.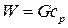 . (16.2)
. (16.2)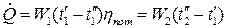 . (16.3)
. (16.3)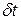 , уравнение (16.3) при
, уравнение (16.3) при  . (16.4)
. (16.4) ,
,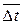 — средние значения коэффициента теплопередачи и температурного напора всего теплообменного аппарата.
— средние значения коэффициента теплопередачи и температурного напора всего теплообменного аппарата. . (16.5)
. (16.5) неизвестен, он определяется из уравнения (16.3).
неизвестен, он определяется из уравнения (16.3).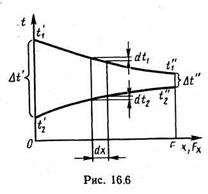
 ;
; . (16.6)
. (16.6)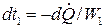 и
и  . Вычитая правые и левые части этих равенств, получим
. Вычитая правые и левые части этих равенств, получим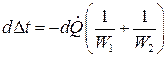 . (16.7)
. (16.7)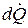 из уравнения (16.6) и разделения переменных найдем
из уравнения (16.6) и разделения переменных найдем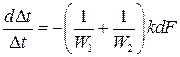 .
. . (16.8)
. (16.8)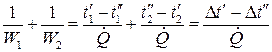 .
. . (16.9)
. (16.9) и
и 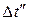 обозначены на рис.16.5).
обозначены на рис.16.5).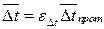 , (16.10)
, (16.10)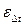 — поправка, которая зависит от двух вспомогательных величин:
— поправка, которая зависит от двух вспомогательных величин: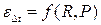 рассчитаны для различных схем движения теплоносителей и приводятся в справочной литературе.
рассчитаны для различных схем движения теплоносителей и приводятся в справочной литературе. и
и  . Например, при
. Например, при 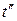 =100°С,
=100°С, 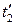 =67,5°С и
=67,5°С и 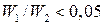 или
или 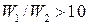 ) и при
) и при  обе схемы становятся равноценными. Первое условие равнозначно несущественному изменению температуры одного из теплоносителей (например, при изменении его агрегатного состояния). При
обе схемы становятся равноценными. Первое условие равнозначно несущественному изменению температуры одного из теплоносителей (например, при изменении его агрегатного состояния). При 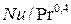 <58 поперечное обтекание позволяет получить больший коэффициент теплоотдачи, чем продольное обтекание труб. Поэтому возможны такие условия, при которых теплообменник с перекрестным током при прочих равных условиях будет иметь меньшую поверхность теплообмена.
<58 поперечное обтекание позволяет получить больший коэффициент теплоотдачи, чем продольное обтекание труб. Поэтому возможны такие условия, при которых теплообменник с перекрестным током при прочих равных условиях будет иметь меньшую поверхность теплообмена. близки по своим значениям, то вместо выражения (16.9) можно воспользоваться формулой среднеарифметического температурного напора:
близки по своим значениям, то вместо выражения (16.9) можно воспользоваться формулой среднеарифметического температурного напора: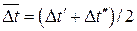 . (16.12)
. (16.12)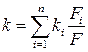 ,
,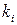 — коэффициент теплопередачи каждого участка;
— коэффициент теплопередачи каждого участка;  — относительная площадь этого участка; п — число участков, на которое разделена рабочая поверхность.
— относительная площадь этого участка; п — число участков, на которое разделена рабочая поверхность.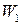 >W2, то
>W2, то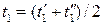 .
.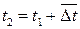 ,
, ,
,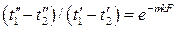 .
.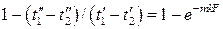 .
. . (16.13)
. (16.13) .
.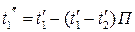 (16.14)
(16.14) . (16.15)
. (16.15)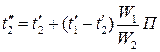 . (16.16)
. (16.16) ; (16.17)
; (16.17)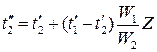 , (16.18)
, (16.18) . (16.19)
. (16.19)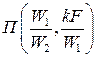 и
и  составлены таблицы [11]. Здесь же рассмотрены приближенные формулы для определения конечных температур теплоносителей в аппаратах с перекрестным током и иными схемами движения.
составлены таблицы [11]. Здесь же рассмотрены приближенные формулы для определения конечных температур теплоносителей в аппаратах с перекрестным током и иными схемами движения.


