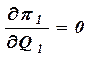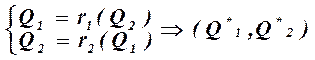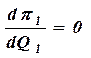Т.е у фирм отсутствуют стимулы, как к входу в данную отрасль, так и к выходу из нее.

При этом

P^*_LR > MR(Q*_LR) = MC(Q*_LR)

Раздел 5. Олигополия

При олигополии основная часть выпуска отрасли производится несколькими крупными фирмами. В силу взаимозависимости поведения предприятий, принимая решение выборе объема выпуска и цены, каждая фирма должна учитывать поведение соперников. Следовательно, кривая спроса на продукцию фирмы не является заданной заранее.

От спроса на продукцию фирмы напрямую зависит предельная выручка фирмы MR, а значит, условие максимизации прибыли MR = MC во многих случаях также не действует.

Участники олигополии могут действовать независимо друг от друга – некооперированная олигополия (non-collusion) или вступать в явный или тайный сговор – кооперированная олигополия (collusion).

Олигополия с двумя фирмами – дуополия.

Модели поведения некооперированной олигополии

· модель Курно

Предположения:

- фирмы выпускают одинаковую продукцию;

- фирмам известна рыночная кривая спроса;

- фирмы принимают решение об объеме выпуска одновременно и самостоятельно;

- каждая фирма считает выпуск соперника заданным, т.е. не меняющимся в ответ на ее собственное решение.

p₁(Q_1,Q₂) = TR₁(Q₁,Q₂) - TC₁(Q₁) = P(Q₁ + Q₂)×Q₁ - TC₁(Q₁) ® max

p₂(Q_1,Q₂) = TR₂(Q₁,Q₂) – TC₂(Q₂) = P(Q₁ + Q₂)×Q₂ – TC₂(Q₂) ® max

MR₁(Q₁,Q₂) = MC₁(Q₁) Þ Q₁ = r₁(Q₂) – функция реакции 1-й фирмы на выпуск 2-й

MR₂(Q₁,Q₂) = MC₂(Q₂) Þ Q₂ = r₂(Q₁) – функция реакции 2-й фирмы на выпуск 1-й

- равновесие

 

Замечания:

- для фирм с одинаковыми функциями затрат Q*₁ = Q*₂ = Q*/2

- при увеличении числа фирм при прочих равных условиях общий выпуск отрасли стремится к объему выпуска совершенно-конкурентной отрасли.

 

· модель Штакельберга

Предположения:

- фирмы выпускают одинаковую продукцию;

- одна фирма – лидер, другая – последователь - принимают решение об объеме выпуска;

- последователь действует согласно своей функции реакции, считая выпуск лидера заданным (аналогично модели Курно);

- лидер знает функцию реакции последователя и использует ее для максимизации своей прибыли.

 

Пусть Q₁, p₁ – выпуск и прибыль лидера,

Q₂, p₂ – выпуск и прибыль последователя.

Q₂ = r₂(Q₁) – функция реакции последователя

Тогда

p₁ = TR₁(Q₁,Q₂) - TC₁(Q₁) = P(Q₁ + Q₂)×Q₁ - TC₁(Q₁) = P(Q₁ + r₂(Q₁))×Q₁ - TC₁(Q₁) ® max

Þ Q*₁, Q*₂ = r₂(Q*₁)

Замечания:

- в случае, если обе фирмы ведут себя как последователи, модель Штакельберга сводится к модели Курно;

- в случае, если обе фирмы ведут себя как лидеры, модель Штакельберга приводит к ценовой войне. Результатом ценовой войны может являться сговор или отказ одной из фирм от стратегии поведения последователя.

· модель Бертрана

Предположения:

- фирмы выпускают одинаковую продукцию;

- фирмам известна кривая рыночного спроса;

- фирмы принимают решение об установлении цены одновременно и самостоятельно;

- каждая фирма считает цену соперника заданной.

Результатом модели Бертрана является равновесие Нэша, характеризующееся единой ценой P* = MC₁ = MC₂. Выпуск отрасли Q* = Q_D(P*).