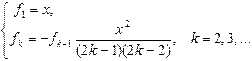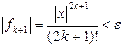ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ПРЕДЕЛА ПОСЛЕДОВАТЕЛЬНОСТИ
Последовательность может иметь предел при n → ∞. Пусть
а слагаемые f k стремятся к нулю при k → ∞.
_________________________________________ S:=a; f:=a; k:=2; while abs(f)>=eps do Begin f:= p (k, f); S:=S+f; k:=k+1 End _________________________________ Трудоемкость программы, т.е. количество k выполнений цикла, определяется из формулы | f k + 1 | < ε. _______________________________________ Приближенное значение функции sin x:
Рекуррентное соотношение для элементов суммы
__________________________________________ S:=x; f:=x; k:=2; while abs(f)>=eps do Begin f:=-f*x*x/((2*k-1)*(2*k-2)); S:=S+f; k:=k+1 End __________________________________________ Трудоемкость алгоритма (количество k выполнений цикла):
Если | x | ≤ 1, ε ≤ 1/2, то k ≤ log2 1/ε. _________________________________________
|