Доказательство. while (x>0)and(y>0) do
Базис. При n = 0 и n = 1 проверяем простой подстановкой. Предположение. Пусть при n ≥ 0 формула верна. Вывод. При n + 1 получаем:
учитывая, что
_________________________________________ Число __________________________________________ Алгоритм Евклида, вычисляющий наибольший общий делитель НОД(a, b) двух целых чисел a ≥ 0, b ≥ 0, основан на инвариантных соотношениях: 1) НОД(a, 0) = a; 2) НОД(a, b) = НОД(b, a); 3) НОД(a, b) = НОД(a mod b, b), a ≥ b > 0. __________________________________________ Докажем третье соотношение. Операция r = a mod b эквивалентна многократному вычитанию b из a до тех пор, пока не будет выполняться 0 ≤ r < b. Поэтому достаточно доказать, что НОД(a, b) = НОД(a – b, b), a ≥ b > 0. Пусть верно противоположное утверждение, а именно: НОД(a, b) = d, НОД(a – b, b) = c, причем c ≠ d. Но тогда __________________________________________ Последовательность пар { xi, yi } такова, что НОД(xi, yi) = НОД(a, b), max(xi, yi) > max(xi + 1, yi + 1)
_________________________________________ x:=a; y:=b; while (x>0)and(y>0) do if x>=y then x:=x mod y else y:=y mod x; if x>0 then nod:=x else nod:=y _________________________________________ Трудоемкость программы определяется числами a и b. Наихудший случай будет, если при fk ≥ max(a, b) > fk – 1, где fk, fk – 1 – числа последовательности Фибоначчи, выполняется условие max(a, b) = fk , min(a, b) = fk – 1 . Тогда k – количество выполнений цикла. Пренебрегая вторым слагаемым в формуле
и логарифмируя левую и правую части, получим:
Т.е. трудоемкость алгоритма Евклида имеет порядок O (log max(a, b)). __________________________________________
|



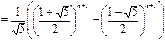
 .
.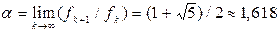 называют золотым сечением.
называют золотым сечением.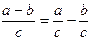 , при этом
, при этом  , а также
, а также 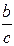 – оба целые, в то время как
– оба целые, в то время как 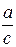 может быть целым лишь в случае, если c = d. Это противоречие и доказывает третье соотношение.
может быть целым лишь в случае, если c = d. Это противоречие и доказывает третье соотношение.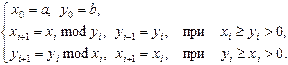

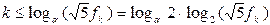 ,
, 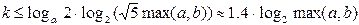 ,
,


